92. R의 Dataset을 이용한 분산분석
Chapter 92. R의 Dataset을 이용한 분산분석
이번회차에는 R에 내장되어 있는 데이터셋을 이용하여 일원배치 분산분석을 정리해보고자 합니다.
R에는 다양한 예제 데이터셋이 내장되어 있어 데이터 분석 연습 및 예제로 활용할 수 있습니다.
data()
내장되어 있는 데이터셋 리스트
1. Dataset 소개
chickwts는 R에 기본으로 포함된 데이터셋 중 하나입니다. 이 데이터셋은 71마리의 병아리에 대한 두 가지 다른 사료 조건에서 12일 동안의 체중을 기록한 것입니다. 데이터셋은 다음과 같이 구성되어 있습니다.
(1) weight: 병아리의 체중(그램).
(2) feed : 병아리에게 제공된 사료의 종류.
"horsebean", "casein", "linseed", "soybean", "sunflower", "meatmeal"
이 데이터셋은 데이터프레임 형식으로 제공되며, 다음과 같이 불러와 사용할 수 있습니다.
data(chickwts)
위 코드를 실행하면 `chickwts` 데이터셋이 `chickwts`라는 변수에 할당됩니다. 이제 이 데이터셋을 자유롭게 분석하고 시각화할 수 있습니다.
head(chickwts) weight feed
1 179 horsebean
2 160 horsebean
3 136 horsebean
4 227 horsebean
5 217 horsebean
6 168 horsebean
dim(chickwts)[1] 71 2
71개의 자료와 2개의 열(column)로 구성되어 있습니다.
2. 데이터 시각화
사료별로 상자그림을 그려보겠습니다.
boxplot(weight~feed,chickwts, boxwex = 0.7
,col=c("skyblue",'orange','green','pink','yellow','purple'))

그림 상으로 평균의 차이는 있을 것으로 생각됩니다.
3. 분산분석표
위 자료에 대한 분산분석표를 구하는 코드는 아래와 같습니다.
summary(aov(weight~feed,data = chickwts)) Df Sum Sq Mean Sq F value Pr(>F)
feed 5 231129 46226 15.37 5.94e-10 ***
Residuals 65 195556 3009
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
위 분산분석표에서 P-value는 5.94e-10 으로 0에 가까운 값이 나타납니다. 따라서, 귀무가설을 기각합니다. 즉, 사료에 따른 체증증가는 유의미한 차이가 있다라고 할 수 있습니다.
4. 등분산성 및 정규성
우선 선형분석을 실행합니다.
result <- lm(weight~feed,data = chickwts)
summary(result)Call:
lm(formula = weight ~ feed, data = chickwts)
Residuals:
Min 1Q Median 3Q Max
-123.909 -34.413 1.571 38.170 103.091
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 323.583 15.834 20.436 < 2e-16 ***
feedhorsebean -163.383 23.485 -6.957 2.07e-09 ***
feedlinseed -104.833 22.393 -4.682 1.49e-05 ***
feedmeatmeal -46.674 22.896 -2.039 0.045567 *
feedsoybean -77.155 21.578 -3.576 0.000665 ***
feedsunflower 5.333 22.393 0.238 0.812495
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 54.85 on 65 degrees of freedom
Multiple R-squared: 0.5417, Adjusted R-squared: 0.5064
F-statistic: 15.36 on 5 and 65 DF, p-value: 5.936e-10
(1) 잔차 검진
잔차그림을 통하여 등분산성에 대한 확인을 해봅니다.
#각 수준의 잔차
resid <- residuals(result) # result$residuals
# 각 수준의 평균
yhat <- fitted(result) # result$fitted.values
# 잔차그림
plot(yhat,resid,xlab=expression(hat(y)),ylab="e",col="navy")
abline(h=0)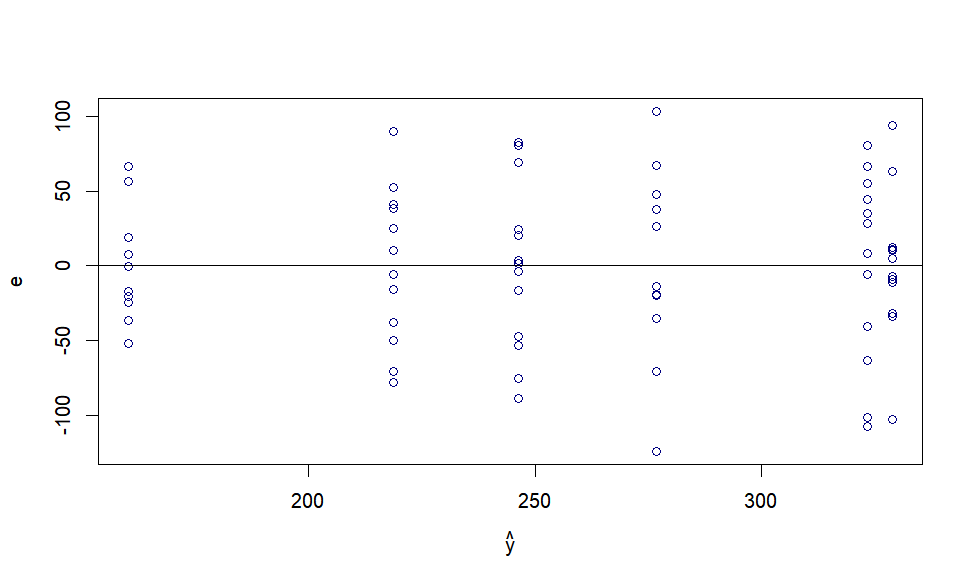
그림상으로는 등분산성을 이루는 것으로 보입니다.
(2) 등분산성- bartlett.test
bartlett.test를 이용하여 수치로 등분산성을 확인해보겠습니다.
bartlett.test(weight~feed,data=chickwts) Bartlett test of homogeneity of variances
data: weight by feed
Bartlett's K-squared = 3.2597, df = 5, p-value = 0.66
P-value는 0.66 으로 귀무가설을 기각하지 못합니다. 즉, 등분산성이 있음을 확인할 수 있습니다.
(3) 정규성 - shapiro.test
shapiro.test(resid)
Shapiro-Wilk normality test
data: resid
W = 0.98616, p-value = 0.6272
P-value는 0.6272 으로 귀무가설을 기각하지 못합니다. 즉, 정규성이 있음을 확인할 수 있습니다.
위 데이터는 등분산성과 정규성을 이루고 있음을 알 수 있습니다.
5. 다중비교
(1) Fisher's LSD
with(chickwts,pairwise.t.test(weight,feed,p.adj="none"))
Pairwise comparisons using t tests with pooled SD
data: weight and feed
casein horsebean linseed meatmeal soybean
horsebean 2.1e-09 - - - -
linseed 1.5e-05 0.01522 - - -
meatmeal 0.04557 7.5e-06 0.01348 - -
soybean 0.00067 0.00032 0.20414 0.17255 -
sunflower 0.81249 8.2e-10 6.2e-06 0.02644 0.00030
P value adjustment method: none
(2) Bonferroni
with(chickwts,pairwise.t.test(weight,feed,p.adj="bonf"))
Pairwise comparisons using t tests with pooled SD
data: weight and feed
casein horsebean linseed meatmeal soybean
horsebean 3.1e-08 - - - -
linseed 0.00022 0.22833 - - -
meatmeal 0.68350 0.00011 0.20218 - -
soybean 0.00998 0.00487 1.00000 1.00000 -
sunflower 1.00000 1.2e-08 9.3e-05 0.39653 0.00447
P value adjustment method: bonferroni
위 두 가지 방법으로 검토한 결과로,
(horsebean),(linseed,soybean),(meatmeal,casein,sunflower) 대략 3부류로 나뉜 것으로 보입니다.
6. 선형대비
사료의 종류를 동물성 사료와 식물성 사료로 나누면,
동물성 사료에는 "casein" , "meatmeal"
식물성 사료는"horsebean", , "linseed", "soybean", "sunflower" 로 분류해서 선형대비를 해보겠습니다.
library(contrast)
contrast(result, list(feed = "casein"),
list(feed = c("sunflower", "soybean","linseed", "horsebean")), type = "average")lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 85.00952 17.72813 49.60401 120.415 4.8 65 0
contrast(result, list(feed = "meatmeal"),
list(feed = c("sunflower", "soybean","linseed", "horsebean")), type = "average")
lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 38.33528 18.3597 1.668431 75.00213 2.09 65 0.0407
동물성 사료와 식물성 사료 사이에 차이가 있음을 알 수 있습니다.
하지만, sunflower와 soybean과 동물성 사료와 비교해보면,
contrast(result, list(feed = c("casein", "meatmeal")),
list(feed = c("sunflower", "soybean")), type = "average")
lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 12.57359 15.73076 -18.84291 43.99009 0.8 65 0.427
차이가 없음을 알 수 있습니다. 따라서, 보다 세부적인 원인을 찾아볼 필요가 있습니다.