| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 정규분포
- 회귀분석
- 해운업
- 데이터 과학
- 산점도
- JavaScript
- 혼합효과모형
- 글쓰기
- html
- 확률
- r
- 경제학
- 통계학
- version 2
- 티스토리챌린지
- 이원배치 분산분석
- 가설검정
- 이항분포
- 분산분석
- 에세이
- css
- 인공지능
- 변동분해
- 반복있음
- version 1
- 오블완
- 고정효과모형
- 추정
- 변량효과모형
- 반복없음
- Today
- Total
생각 작업실 The atelier of thinking
68. 모분산에 대한 통계적 추론 본문
통계적 추론은 추론 목적에 따라 크기 추정과 가설검정으로 나눌 수 있습니다.

통계적 추론은 일반적으로 모집단의 특성에 대한 정보를 표본으로부터 얻어내는 과정을 포함합니다. 특히, 모평균과 모분산은 통계적 추론에서 주로 다루어 지는 대상들 입니다.
표본으로부터 얻은 통계량을 사용하여 모집단의 특성에 대한 가설을 검정하거나, 신뢰구간을 구하여 추정하는 등의 작업을 수행하여 통계적 추론을 실시합니다.
1. 모분산에 대한 통계적 추론
모분산에 대한 통계적 추론은 표본을 사용하여 모집단의 분산에 대한 추론을 수행하는 과정을 말합니다. 이를 통해 모집단의 분산에 대한 정보를 얻을 수 있고, 추론 결과를 통해 모집단의 분산에 대한 결론을 도출할 수 있습니다.
통계적 추론에서 모분산에 대한 추론은 주로 가설 검정과 구간 추정의 형태로 이루어집니다.
(1) 모분산에 대한 추정
구간 추정은 모분산에 대한 신뢰구간을 구하여 모수의 추정 범위를 제공합니다. 즉, 표본을 사용하여 계산한 신뢰구간을 통해 모집단의 분산이 존재할 가능성을 추정하는 것입니다. 이를 통해 모분산의 신뢰구간을 구성하고, 모집단의 분산에 대한 추론을 수행할 수 있습니다.
(2) 모분산에 대한 가설검정
가설 검정은 모집단의 분산에 대한 가설을 설정하고, 표본을 통해 얻은 통계량을 사용하여 가설을 검정하는 과정입니다. 대표적인 예로는 분산의 크기가 특정 값과 같은지 여부를 검정하는 분산 검정이 있습니다.
모분산에 대한 통계적 추론은 데이터의 변동성에 대한 추정과 관련된 중요한 분야입니다. 이를 통해 표본을 통해 얻은 정보를 활용하여 모집단의 분산에 대한 결론을 도출하고, 신뢰성 있는 추론을 수행할 수 있습니다.
2. 모집단 가정
기본적으로 우리가 분산에 대한 추론을 할 때 모집단에 대한 가정은 정규분포를 가정합니다.
따라서 정규분포를 만족하는지 안하는지 확인할 필요가 있습니다. 정규분포가 아닌 경우에 약간 문제가 발생할 수도 있습니다.
(1) 확률표본
정규 모집단에서 추출한 확률표본은 정규분포를 나타냅니다.
$$X_1,X_2,...,X_n\sim iid N (\mu ,\sigma ^2) $$
(2) 점추정
모수인 모분산에 대한 정보는 표본분산이 가장 많이 가지고 있으므로 직관적으로 표본분산을 사용합니다. 모표준편차는 표본표준편차를 사용합니다.
모수 : $\sigma^2$ → 표본분산 : $S^2 = \frac{1}{n-1} \sum_{i=1}^n(X_i - \bar{X})^2 $
모수 : $\sigma$ → 표본표준편차 : $S = \sqrt{\frac{1}{n-1} \sum_{i=1}^n(X_i - \bar{X})^2} $
점 추정량의 통계적 성질은 아래와 같습니다.
$$ E(S^2) = \sigma^2 $$
$$ Var(S^2) = \frac{2\sigma^4}{(n-1)} $$
수정 제곱합을 분산으로 나누면, 카이제곱분포를 따른다고 알려져 있습니다.
$$ \frac{(n-1)S^2}{\sigma^2} = \frac{\sum_{i=1}^n(X_i-\bar{X})^2}{\sigma^2} \sim \chi^2_{n-1} $$
$ \chi^2_{n-1} $ : 자유도가 $n-1$ 인 카이제곱분포(chi-square distribution)
(3) 중심축량
모평균 추론에서와 같이 모분산추론을 위해서 중심축량에 대해 알아야 합니다. 중심축량은 점추정을 통해 구하는 데 직관적인 추정량으로 표본분산 및 표본표준편차를 사용합니다.
따라서 분산과 표준편차의 구간추정과 가설검정을 시행함으로 추론할 수 있습니다.
$$ \frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1} $$
(4) 카이제곱분포 (Chi-square Distribution)
2023.12.20 - [통계학 이야기] - 59. 카이제곱분포(Chi-square Distribution) - 연속확률분포
59. 카이제곱분포(Chi-square Distribution) - 연속확률분포
Chapter 59. 카이제곱분포(Chi-square Distribution) - 연속확률분포 1. 카이제곱분포란? k개의 서로 독립적인 표준정규확률변수를 각각 제곱한 다음 합해서 얻어지는 분포입니다. k를 자유도라고 하며 카
thinking-atelier.tistory.com
카이제곱분포는 k개의 서로 독립적인 표준정규확률변수를 각각 제곱한 다음 합해서 얻어지는 분포입니다.
k를 자유도라고 하며 카이제곱분포의 매개변수가 됩니다. 카이제곱분포는 신뢰구간이나 가설검정에서 사용합니다.
3. 모분산의 구간 추정
앞서 카이제곱분포에서 양측 검정시 임계값은 구간거리 최소보다는 양측 검정에 비교적 찾기 쉬운 $\alpha/2$ 을 사용합니다.
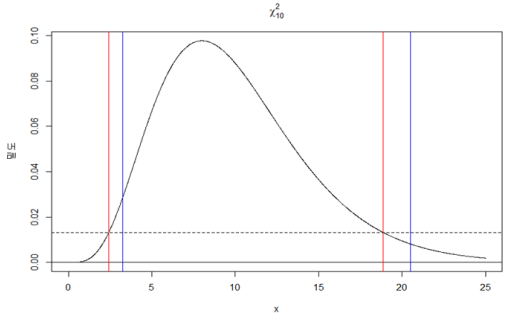
모분산에 대한 구간 추정은 카이제곱분포를 이용하여 구할 수 있습니다.
$$ \frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1} $$
모분산의 구간 추정은 위 중심축량을 기준으로 신뢰구간을 정하게 됩니다.
유도과정을 살펴보면 아래와 같습니다.
▶ 모분산의 $100(1 - \alpha)%$ 신뢰구간
$$ 1 - \alpha = P \left( \chi^2_{1-\alpha/2,n-1} \le \frac{(n-1)S^2}{\sigma^2} \le \chi^2_{\alpha/2,n-1} \right) $$
$$= P \left( \frac{(n-1)S^2}{\chi^2_{\alpha/2,n-1}} \le \sigma^2 \le \frac{(n-1)S^2}{\chi^2_{1-\alpha/2,n-1}} \right) $$
따라서, 신뢰구간은 아래와 같이 정리할 수 있습니다.
$$ \left( \frac{(n-1)S^2}{\chi^2_{\alpha/2,n-1}} , \frac{(n-1)S^2}{\chi^2_{1-\alpha/2,n-1}} \right) $$
▶ 모표준편차의 $100(1 - \alpha)%$ 신뢰구간
$$ \left( \sqrt{\frac{(n-1)S^2}{\chi^2_{\alpha/2,n-1}}} ,\sqrt{ \frac{(n-1)S^2}{\chi^2_{1-\alpha/2,n-1}}} \right) $$
◈ 예제 : 제품강도
생산된 제품의 강도가 어느 수준에서 안정적으로 생산되는지 알아보기 위해 임의로 8개를 선택하여 제품강도를 측정합니다. 일반적으로 안정성은 분산으로 평가합니다.
제품 강도 결과 : 24.3 , 28.6, 30.2, 26.5, 25.7, 27.8, 26.9, 29.0
모분산과 모표준편차의 95% 신뢰구간은 ?
$$ \left( \frac{(n-1)S^2}{\chi^2_{\alpha/2,n-1}} , \frac{(n-1)S^2}{\chi^2_{1-\alpha/2,n-1}} \right) $$
표본분산 $S^2 - 3.65 $
유의수준 5% 인 양측 검정 카이제곱 분위수는 0.025, 0.975 의 값은 ?
$$ \chi^2_{0.025,7} = 1.690 , \chi^2_{0.975,7} = 16.013 $$
▶ 모분산의 95% 신뢰구간
위에서 구한 값을 적용하면,
$$ \left( \frac{7 \times 3.65}{16.013} , \frac{7 \times 3.65}{1.690} \right) = (1.596,15.122) $$
▶ 모표준편차의 95% 신뢰구간
$$ (\sqrt{1.596}, \sqrt{15.122} ) = (1.263, 3.889) $$
4. 가설검정
가설검정의 절차를 살펴보면, 가설을 설정하고 검정통계량을 구하고 구한 검정통계량의 분포와 유의수준을 비교 검토후 기각 또는 채택의 결론을 내리게 됩니다.
(1) 가설 설정
귀무가설$(H_0)$ : 현상태에 대한 잠정적 가정
대립가설 $(H_1)$ : 우리가 알고 싶은 것
$$H_0:\ \sigma ^2=\sigma _0^2\quad vs\quad H_1:\ \begin{cases}\sigma ^2>\sigma _0^2\\\sigma ^2<\sigma _0^2\\\sigma ^2\ne \sigma _0^2\end{cases}$$
(2) 검정 통계량 : 귀무가설하에서 표본의 비정상성을 결정하기 위해 사용되는 통계량
$$ X^2_0 = \frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1} $$
(3) 검정통계량의 분포와 유의수준을 비교 검토합니다.
유의수준을 $\alpha$ 라고 하면 기각역은 $\begin{cases}①[\chi^2_{\alpha ,n-1},\infty )\\②(0,\ \chi^2_{\alpha ,n-1}]\\③(0,\ \chi^2_{1-\alpha /2,n-1}],[\chi^2_{\alpha /2,n-1},\infty )\end{cases}$
(4) 결론
기각역(비정상영역) : 귀무가설 기각 (대립가설 채택)
채택역(정상영역) : 귀무가설 유지 (대립가설 기각)
'통계학 이야기' 카테고리의 다른 글
| 70. 모비율에 대한 통계적 추론 I (1) | 2024.06.11 |
|---|---|
| 69. R을 이용한 카이제곱분포 및 모분산 추정 (2) | 2024.06.10 |
| 67. R을 이용한 모평균에 대한 통계적 추론 (2) | 2024.06.08 |
| 66. 모평균에 대한 통계적 추론 III (1) | 2024.06.07 |
| 65. 모평균에 대한 통계적 추론 II (0) | 2024.02.18 |




