106. 회귀분석 - 예측값과 관측값

Chapter 106. 회귀분석 - 예측값과 관측값

 

1. 예측값과 관측값

 

회귀분석에서 예측값이란 회귀분석 모델이 분석해서 예측한 값을 말합니다. 관측값은 실제 데이터에서 직접 수집하거나 측정한 값입니다. 그리고 예측값과 관측값의 차이를 잔차라고 한다. 이 잔차가 작을 수록 회귀분석 모델의 성능이 좋다고 말할 수 있다.

 

회귀분석의 목적은 예측값과 관측값의 차이를 최소화하는 모델을 만드는 것이다.

 

단순선형 회귀모형은 아래와 같습니다.

 

$$Y_i = \beta_0 + \beta_1x_i + \epsilon_i$$

$$ \epsilon_i \sim iid N(0,\sigma^2)$$

 

위 모형을 그림으로 나타내면, 아래와 같습니다.

 

 

 

① 은 최소제곱법을 이용하여 구한 직선입니다.

② 는 ① 선상위의 값으로 예측값을 말합니다.

③ 은 잔차로서 관측값($y_i$)과 에측값의 차이입니다.

---

 

2. 예측값 평균에 대한 통계적 추론

 

(1) 반응변수(예측값)의 기대값에 대한 추론

 

 예측값의 기대값은 예측값 평균이라 할 수 있습니다.

 

 

새로운 설명변수 x에 대한 반응변수(예측값) y의 기대값은 아래와 같이 나타낼 수 있습니다.

 

$$ E(Y_k) = \beta_0 + \beta_1x_k $$

 

위 그래프 선 위에 위치할 것으로 예상할 수 있습니다. 따라서, 점 추정량은 아래와 같이 표현할 수 있습니다.

 

$$ \hat{Y_k}=\hat{\beta_0}+\hat{\beta_1}x_k $$

 

(2) 점 추정량의 통계적 성질

 

 점 추정량은 예측값($Y_i$)들의 선형결합입니다. 아래와 같이 증명할 수 있습니다.

 

$$ \hat{Y_k}=\hat{\beta_0}+\hat{\beta_1}x_k $$

$$ =(\bar{Y}-\hat{\beta_1}\bar{x}) + \hat{\beta_1}x_k$$

$$ =\bar{Y}+(x_k - \bar{x})\hat{\beta_1}$$

$$ =\bar{Y}+(x_k-\bar{x})\frac{S_{xY}}{S_{xx}} $$

$$ =\sum \left(\frac{1}{n}+(x_k-\bar{x})\frac{(x_i-\bar{x})}{S_{xx}} \right) Y_i $$

 

$Y_i$는 정규분포를 따른다.

$$ Y_i \sim N(\beta_0 + \beta_1 x_i , \sigma^2)$$

 

예측값($Y_i$)이 정규분포를 따르기 때문에 예측값 ($Y_i$) 평균의 점 추정량 역시 정규분포를 따른다고 할 수 있습니다.

 

점 추정량의 기대값과 분산은 아래와 같습니다.

 

$$E(\hat{Y_k}) = E(\hat{\beta_0}+\hat{\beta_1}x_k) = \beta_0 + \beta_1x_k$$

$$Var(\hat{Y_k}) = \sigma^2 \sum \left( \frac{1}{n} + (x_k - \bar{x})\frac{(x_i - \bar{x})}{S_{xx}} \right)^2 $$

$$ = \sigma^2 \left( \frac{1}{n} + \frac{(x_k - \bar{x})^2}{S_{xx}} \right) $$

 

따라서, 점 추정량은 아래와 같이 정규분포를 따릅니다.

 

$$ \hat{Y_k} \sim N \left( \beta_0+\beta_1x_k, \sigma^2 \left( \frac{1}{n} + \frac{(x_k - \bar{x})^2}{S_{xx}} \right) \right)) $$

 

 

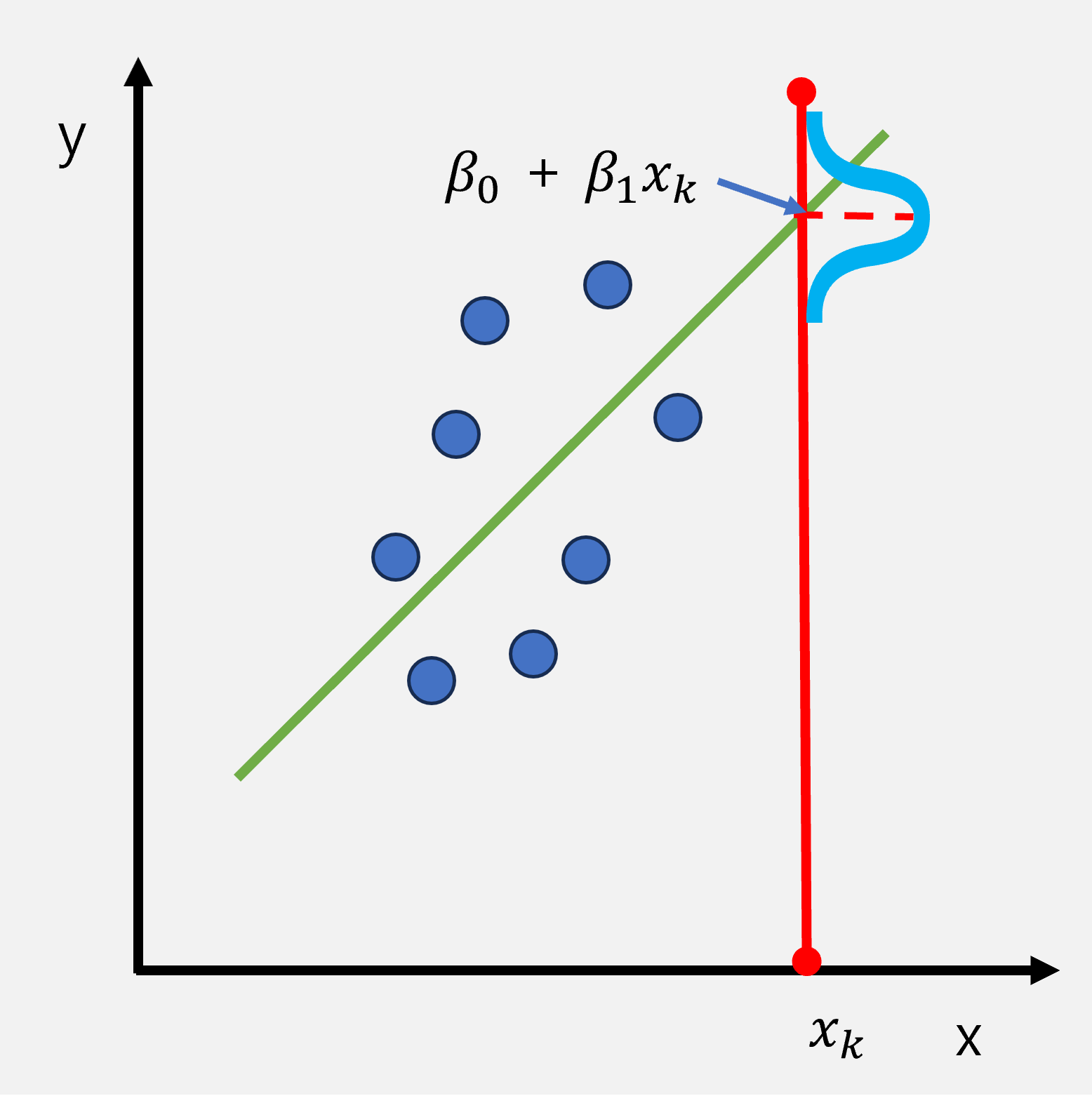
점추정량의 기대값은 선을 기준으로 정규분포를 이루는 모습으로 나타납니다.

 

(3) 중심축량

 

모분산 $\sigma^2$은 알 수 없으므로 MSE를 대신 사용합니다.

 

$$\frac{\hat{Y_k} - E(Y_k)}{\sqrt{MSE} \sqrt{\frac{1}{n}+\frac{(x_k - \bar{x})^2}{S_{xx}}}} \sim t_{n-2}$$

 

중심축량은 자유도 n-2인 t-분포를 따릅니다.

 

(4) 구간 추정

 

$100(1-\alpha)%$ 신뢰구간은 아래와 같습니다.

 

$$ \hat{Y_k} \pm t_{\alpha/2 , n-2} \sqrt{MSE} \sqrt{\frac{1}{n} + \frac{(x_k - \bar{x})^2}{S_{xx}}} $$

 

---

3. 새로운 관측값에 대한 통계적 추론

 

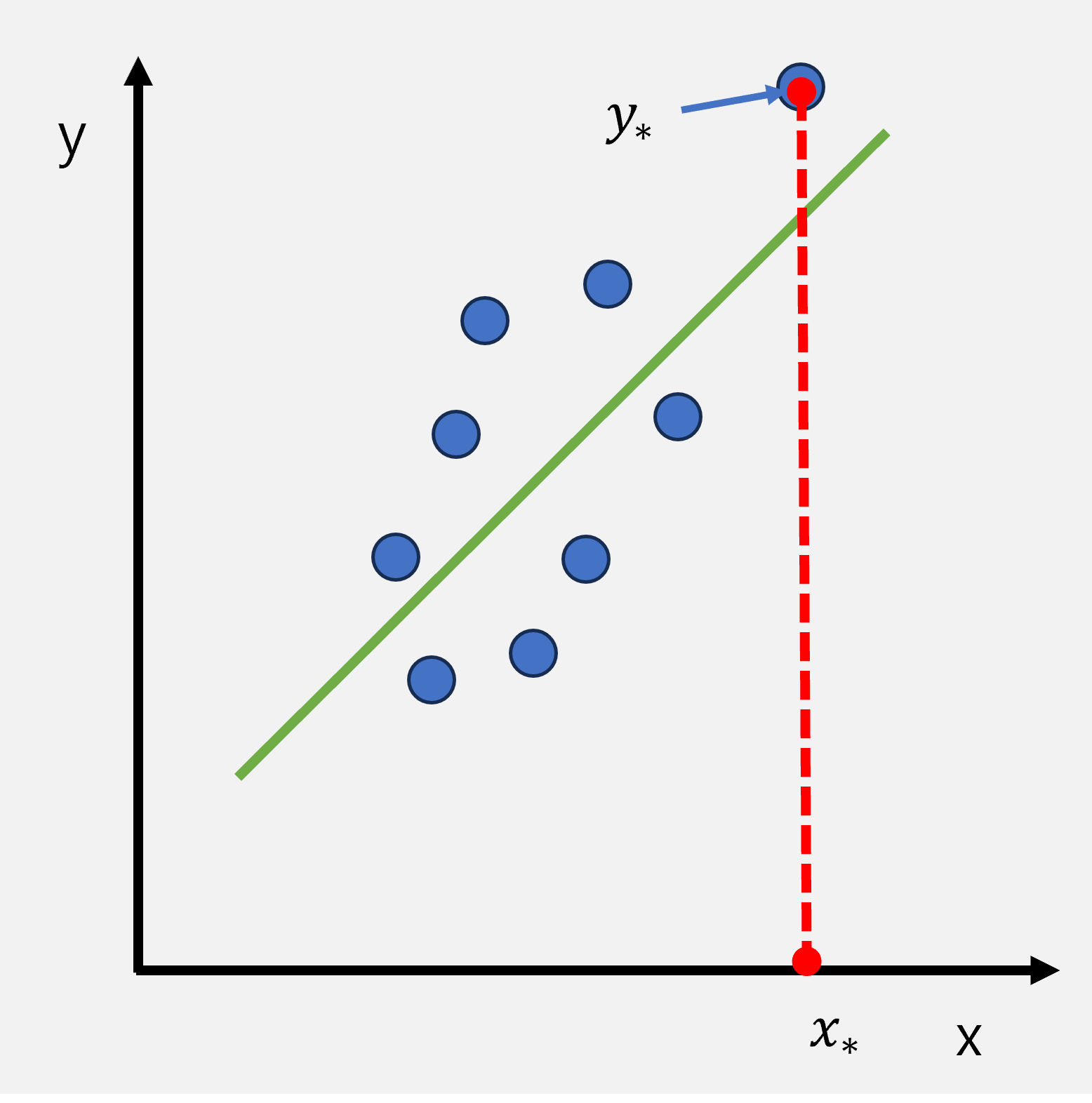
(1) 반응변수 예측값에 대한 추론

 

반응변수의 예측값은 새로운 관측값이라 말할 수 있습니다.