| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 글쓰기
- 통계학
- 산점도
- 반복없음
- 이항분포
- 분산분석
- 티스토리챌린지
- version 2
- 변량효과모형
- 고정효과모형
- JavaScript
- 오블완
- 경제학
- 이원배치 분산분석
- html
- r
- 반복있음
- 혼합효과모형
- 가설검정
- css
- 추정
- 에세이
- version 1
- 두 평균의 비교
- 확률
- 변동분해
- 정규분포
- 회귀분석
- 인공지능
- 데이터 과학
- Today
- Total
생각 작업실 The atelier of thinking
16. 수치 자료의 중심 - 평균의 한계 본문
Chapter 16. 수치 자료의 중심 - 평균의 한계


1. 평균의 한계
평균은 데이터의 중심을 대표하는 대표값 중 하나이지만, 모든 경우에서 좋은 대표값이 될 수는 없습니다.
평균이 한계를 보이는 때는 다음과 같습니다.

(1) 이상점(outlier)에 민감합니다.
이상치는 데이터 집합의 값 중에서 다른 값들과 동떨어져 있는 값으로, 평균을 구할 때 이상치가 포함되면 평균 값이 크게 영향을 받게 됩니다.
(2) 분포의 형태에 따라 왜곡될 수 있습니다.
데이터가 한쪽 방향을 치우쳐져 있거나, 두 개 이상의 그룹으로 나뉘어져 있을 경우에는 평균이 전체 데이터의 대표값이 아닐 수 있습니다.
(3) 비교할 때 주의가 필요합니다.
두 집단의 평균을 비교할 때에는 데이터 분포의 형태와 이상치의 영향을 고려해야 합니다. 또한 집단의 크기가 다르면 평균을 비교하는 것이 공정하지 않을 수 있습니다. 이러한 경우에는 중앙값이나 백분위수를 사용하는 것이 더 적합합니다.
따라서 평균을 사용할 때에는 이러한 한계를 인지하고, 데이터의 특성과 목적에 따라 적절한 대표값을 선택해야 합니다.
2. 이상점(outlier)
예를 들어, " 100,110,120,130,140,120,120,800" 8개 자료의 평균은 205가 나옵니다. 800을 제외하면 평균은 120이 나옵니다. 여기서 800 이라는 숫자는 다른 숫자들과 많이 떨어져 있어 평균의 값을 크게 높여줍니다. 이렇듯 대부분의 관측값으로부터 멀리 떨어져 있는 일부 관측값을 이상점이라고 합니다.
이상점의 포함여부에 따라 평균의 값이 크게 차이가 날 수 있습니다. 이 말인즉, 자료분석에 있어 왜곡현상을 만들어 낼 수 있다는 의미입니다.
이러한 평균의 한계를 대체 하기 위한 통계값으로 중앙값, 절사평균, 최빈값 등을 사용할 수 있습니다.
로버스트(Robust) 의 사전적 의미는 "강건한"이란 뜻입니다. 통계학에서는 이상점에 영향을 받는지 받지 않는지에 대한 표현에 쓰입니다. 로버스트한 통계량이라 한다면 이상점에 영향을 받지 않는다라는 의미입니다. 따라서 평균은 로버스트하지 않은 통계량이라 할 수 있습니다.
◈ 평균의 한계를 보여주는 동영상 : EBS 지식채널 "48분의 함정"
https://www.youtube.com/watch?v=mo9wfhY35I4
3. 심슨의 역설 (Simpson's Paradox)
심슨의 역설이란 데이터의 세부 그룹별로 일정한 추세나 경향성이 나타나지만, 전체적으로 보면 그 추세가 사라지거나 반대방향의 경향성이 나타나는 현상을 의미합니다.
◈ 사례 : 버클리 대학은 대학원 입시에서 성차별을 하였나?
1970년대 미국 버클리대학은 대학원 입시에서 성차별이 있었다는 문제 제기를 받게 됩니다. 그 해 대학원 입시 결과에서 남학생들의 합격률은 45%, 여학생들의 합격률은 30% 였습니다.
대학원 입시는 각 학과에서 관리를 하기 때문에 대표적인 6개 전공에서 남학생과 여학생의 합격률을 비교한 결과는 다음과 같았다고 합니다.
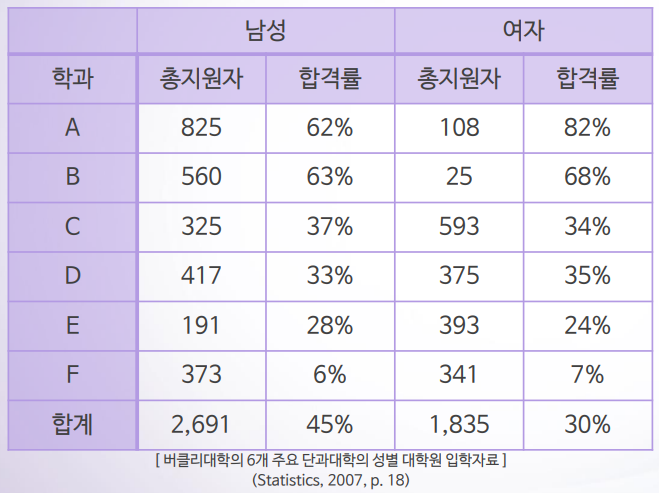
전체 합격률은 남학생이 높았지만, 학과별 합격률은 오히려 여학생이 높아 보입니다.
이렇게 전체합격률과 학과별 합격률이 차이나는 이유는 남학생들은 다수가 합격률이 높은 A,B학과에 지원하였지만, 여학생들은 극소수가 이들학과에 지원하였습니다. 따라서 여학생 전체합격률은 주로 C,D,E,F 학과 합격률에 의해 결정되었고, 남학생들의 전체합격률은 A,B 학과의 높은 합격률에 힘입어 상승하였습니다.
이렇게 제 3의 요인으로 전체자료를 세분화했을 때 정반대의 결과가 나오는 것을 심슨의 역설(Simpon's Paradox)라고 합니다.
이 예제에서 주목할 점은 학과와 합격률, 그리고 학과와 성별 지원자 수 사이에 강한 연관성이 있어서 전체 성별 합격률에 영향을 미쳤다는 점입니다.
◈ 교락 효과(Confounder Effect)
교락 요인(Confounder Effect)는 앞의 예제에서 같이 반응변수(합격 여부)와 설명변수(성별)에 모두 영향을 미치는 변수(학과)를 말합니다.
교락 요인을 통제하여야만 반응변수가 순수하게 설명변수에 미치는 영향을 알 수 있습니다.
교락 요인을 통제하기 위해서 교락 요인의 값에 따라 그룹을 나눈 후 반응변수와 설명변수의 관계를 알아봅니다.(sbugroup analysis). 가중평균을 사용합니다.
◈ 사례 : 버클리 대학은 대학원 입시에서 성차별을 하였나?
이 사례에서 남성 지원자의 가중치를 반영한 합격률(가중평균)을 구하면,
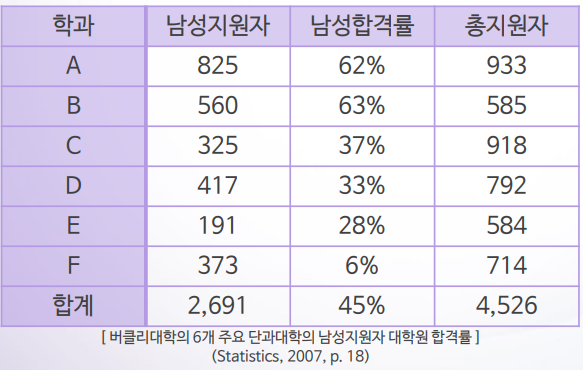
전체 지원자 중 그 학과에 지원하는 사람의 비율을 가중치로 한 후 가중치를 학과별 합격률에 곱하여 남학생의 가중치를 반영한 합격률을 구하면 됩니다. 앞서 가중치 없이 계산한 남성지원자의 합격률은 평균 45% 였습니다. 그러나, 가중치를 반영한 합격률은 39% 가 나오는 것을 볼 수 있습니다.
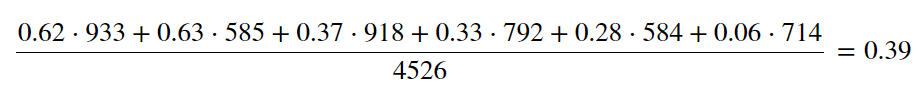
즉, 학과별로 지원하는 남녀 지원자 숫자가 다르다는 점을 통제하기 위해 성별 지원자 비율이 아닌 전체비율을 가중치로 사용하는 것입니다.
여학생의 경우 같은 방법으로 가중치를 구하면 43%가 나옵니다. 오히려 여학생의 합격률이 더 높게 나옵니다.
'통계학 이야기' 카테고리의 다른 글
| 18. 수치자료의 산포 - 분산, 표준편차,분위수 (0) | 2023.09.11 |
|---|---|
| 17. R을 이용한 수치자료의 중심 구하기 (1) | 2023.09.09 |
| 15. 수치 자료의 중심 - 평균, 중앙값, 최빈값 (0) | 2023.09.05 |
| 14-2. R 을 이용한 자료 요약 (0) | 2023.09.01 |
| 14-1. R 을 이용한 자료 요약 (0) | 2023.08.31 |




