생각 작업실 The atelier of thinking
88. R을 이용한 분산분석(ANOVA) 본문
Chapter 88. R을 이용한 분산분석(ANOVA)
1. 일원배치 분산분석
분산분석(ANOVA, Analysis of Variance)은 세 개 이상의 그룹 간의 평균차이를 비교 하는 통계적 기법입니다.
일원배치 분산분석(One-way ANOVA)은 한 개의 설명(독립)변수(요인)가 하나의 반응(종속)변수에 미치는 영향을 분석하는 통계 기법입니다. 일원배치 분산분석에서는 독립변수가 세 개 이상의 수준(그룹)을 가지며, 각 수준에서의 종속변수의 평균을 비교하여 그룹 간의 차이가 통계적으로 유의한지를 검정합니다.
◈ 예제 : 사료에 따른 체중증가 실험
이 실험에서 독립변수(요인)은 사료입니다. 그룹 혹은 수준(처리)의 수는 4 종류이고, 반응변수(종속변수)는 체증증가라고 할 수 있습니다.
실험 대상으로 쥐를 선정하고 할당하는 과정은 완전확률화 설계에 따라 랜덤(random)하게 이루어져야 합니다.
이 때 비교대상은 4종류 사료별 체증증가의 평균이 됩니다.
| 방법 | 쇠고기 저단백 |
쇠고기 고단백 |
시리얼 저단백 |
시리얼 고단백 |
| 반복 | 90 76 90 64 86 51 72 90 95 78 |
73 102 118 104 81 107 100 87 117 111 |
107 95 97 80 98 74 74 67 89 58 |
98 74 56 111 95 88 82 77 86 92 |
| 합 | 792 | 1000 | 839 | 859 |
요인 : 사료, 수준(처리)의 수 : 4 , 반응변수 : 체중증가
반복수 : 각 10 회
2. R을 이용한 일원배치 분산분석
(1) 자료 불러오기
rats <- read.csv("rats.csv",header = TRUE, fileEncoding = "CP949",
encoding = "UTF-8")
head(rats)
사료 체중증가
1 1 90
2 2 73
3 3 107
4 4 98
5 1 76
6 2 102
▶ 사료 부문의 자료를 살펴보면,
rats$사료
[1] 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3
[40] 4
위 자료는 숫자형이므로 범주형 자료로 바꾸어야 합니다. 이 때, 필요한 R의 함수는 as.factor( ) 입니다.
▶ Data의 범주화
as.factor(rats$사료)[1] 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3
[40] 4
Levels: 1 2 3 4
Levels : 1 2 3 4 로 4개의 범주로 바뀌었음을 알 수 있습니다.
(2) 시각화
시각화를 위하여 각 사료별로 상자그림을 그려보는 코드입니다.
rats$사료 <- as.factor(rats$사료)
boxplot(체중증가~사료,rats, col=c("skyblue",'orange','green','pink'))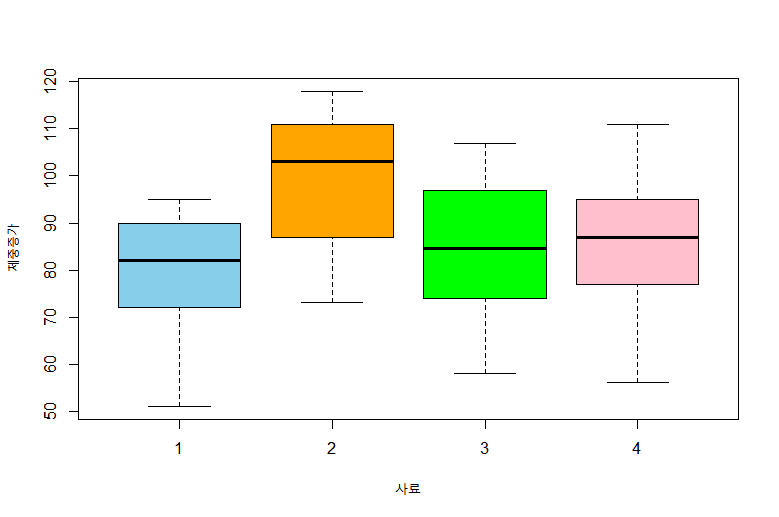
범주화된 자료로 변경시킨 후 이 자료를 이용해 상자그림을 그립니다.
위 그림에서 2번 사료의 체중증가 평균이 다른 사료의 체중증가 평균보다 높은 것으로 보입니다. 이것이 통계적으로 의미있는 차이가 있는 지 알아보기 위해 분산분석을 사용해 보겠습니다.
(3) 분산분석 - aov( ) 함수
aov( ) 함수는 분산 분석(ANOVA)을 수행하는 데 사용됩니다. 이 함수는 하나 이상의 독립 변수(요인)가 종속 변수에 미치는 영향을 평가하고, 그룹 간의 평균 차이가 통계적으로 유의한지를 검정합니다.
aov(formula, data)
formula: 분석할 모델을 지정하는데 사용됩니다.
일반적으로 종속 변수와 독립 변수 간의 관계를 나타내는 공식으로 지정됩니다.
data: 분석에 사용할 데이터 프레임을 지정합니다.
위 자료를 분산분석을 하면,
aov(체중증가~사료,data=rats)
Call:
aov(formula = 체중증가 ~ 사료, data = rats)
Terms:
사료 Residuals
Sum of Squares 2404.1 8049.4
Deg. of Freedom 3 36
Residual standard error: 14.95307
Estimated effects may be unbalanced
결과값에 대한 설명은 아래와 같습니다.
● Call: 사용된 함수의 호출 방식과 사용된 인수들을 나타냅니다.
● Terms: 모델에 사용된 요인들에 대한 분산 분석 결과를 보여줍니다. 여기서 "사료"는 사용된 요인이며, "Residuals"는 오차 항목을 나타냅니다. 각각의 항목에 대해 제곱합과 자유도가 제공됩니다.
● Sum of Squares: 각 항목에 대한 제곱합(합의 제곱)을 나타냅니다.
● Deg. of Freedom: 각 항목에 대한 자유도를 나타냅니다.
● Residual standard error: 모델의 잔차 표준 오차를 나타냅니다. 이 값은 모델이 관찰된 데이터를 얼마나 잘 설명하는지에 대한 측정입니다.
● Estimated effects may be unbalanced: 사용된 효과의 추정치가 균형이 없을 수 있다는 경고입니다. 이는 데이터셋이 그룹 간에 불균형하게 분포되어 있을 수 있다는 것을 나타냅니다. 이 경우 분산 분석 결과의 해석에 유의해야 합니다.
위 내용만으로는 검정통계량이 나와있지 않기 때문에 추가로 summary( ) 함수를 사용합니다.
summary(aov(체중증가~사료,data=rats))
Df Sum Sq Mean Sq F value Pr(>F)
사료 3 2404 801.4 3.584 0.023 *
Residuals 36 8049 223.6
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
● Mean Sq: 평균 제곱을 나타냅니다. 이 값은 제곱합을 해당 자유도로 나눈 것입니다.
● F value: F-통계량을 나타냅니다. 이 값은 "사료" 그룹 간의 분산과 잔차의 분산 비율에 대한 통계량입니다. 즉, 그룹 간의 차이가 오차의 변동에 비해 얼마나 큰지를 나타냅니다.
● Pr(>F): F-통계량에 대한 p-value를 나타냅니다. 이 값은 "사료" 그룹 간의 평균이 통계적으로 유의하게 다른지를 판단하는 데 사용됩니다. 만약 p-value가 유의수준(예: 0.05)보다 작으면, "사료" 그룹 간의 평균이 통계적으로 유의하게 다르다는 것을 의미합니다. 여기서는 p-value가 0.023이므로 유의수준 0.05에서 "사료" 그룹 간의 평균이 통계적으로 유의하게 다르다고 볼 수 있습니다.
또한, Signif. codes는 p-value의 유의성을 나타내는 코드를 표시합니다. 일반적으로 별표가 많을수록 p-value가 유의하다는 것을 의미하며, '*'가 하나인 경우 0.05보다 작은 유의성을 나타냅니다.
summary( aov( ) ) 함수는 아래의 분산분석표를 보여줍니다.
| 변동요인 | 자유도 | 제곱합 | 평균제곱 | F-통계량 |
| 처리(모형) | p-1 | SSTR | MSTR | MSTR/MSE |
| 오차 | N-p | SSE | MSE | |
| 전체 | N-1 | TSS |
(4) 분산분석 - lm( ) 함수
분산분석을 하는 또 다른 방법은 선형 모델을 이용하는 방법입니다.
선형회귀분석함수는 lm( ) 이 있습니다.
lm(formula, data)
formula: 분석할 모델을 지정하는데 사용됩니다.
일반적으로 종속 변수와 독립 변수 간의 관계를 나타내는 공식으로 지정됩니다.
data: 분석에 사용할 데이터 프레임을 지정합니다.
위 자료를 분산분석을 하면,
lm(체중증가~사료,data=rats)
Call:
lm(formula = 체중증가 ~ 사료, data = rats)
Coefficients:
(Intercept) 사료2 사료3 사료4
79.2 20.8 4.7 6.7
● (Intercept): 절편을 의미합니다. 이는 다른 모든 설명 변수가 0일 때의 예측된 종속 변수의 값입니다. 여기서는 사료1의 평균이라 할 수 있습니다.
● 사료2, 사료3, 사료4: "사료" 변수의 수준에 대한 회귀 계수입니다. 여기서 "사료" 변수는 범주형이며, 더미 변수화되어 각 수준에 대해 하나의 회귀 계수가 할당됩니다.
해석은 다음과 같습니다:
● 사료2: 사료 2를 뜻하며, 다른 모든 설명 변수가 동일할 때 사료 2를 사용하는 경우, 종속 변수의 평균적인 증가량은 20.8이라고 해석할 수 있습니다.
● 사료3: 사료 3을 뜻하며, 다른 모든 설명 변수가 동일할 때 사료 3을 사용하는 경우, 종속 변수의 평균적인 증가량은 4.7이라고 해석할 수 있습니다.
● 사료4: 사료 4를 뜻하며, 다른 모든 설명 변수가 동일할 때 사료 4를 사용하는 경우, 종속 변수의 평균적인 증가량은 6.7이라고 해석할 수 있습니다.
이러한 회귀 계수는 각각의 사료 유형이 종속 변수에 미치는 영향을 나타냅니다. 만약 사료 유형이 종속 변수와 관련이 있다면, 해당 사료 유형의 회귀 계수는 0이 아닌 유의한 값으로 나타날 것입니다.
위 선형회귀함수에 추가로 anova( ) 함수를 사용합니다.
result <- lm(formula, data)
anova(result)Analysis of Variance Table
Response: 체중증가
Df Sum Sq Mean Sq F value Pr(>F)
사료 3 2404.1 801.37 3.584 0.02297 *
Residuals 36 8049.4 223.59
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
위 summary( aov( ) ) 함수와 같은 결과값이 나옵니다.
다만, anova( ) 함수에는 선형모델 데이터 값이 들어가야 하기 때문에 기존 데이터를 선형모델하는 것이 선행되어야 합니다.
참고로 위 선형회귀함수에 추가로 summary( ) 함수를 사용하면 아래와 같은 결과값이 나옵니다.
result <- lm(체중증가~사료,data=rats)
summary(result)
Call:
lm(formula = 체중증가 ~ 사료, data = rats)
Residuals:
Min 1Q Median 3Q Max
-29.90 -9.90 2.05 10.85 25.10
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 79.200 4.729 16.749 < 2e-16 ***
사료2 20.800 6.687 3.110 0.00364 **
사료3 4.700 6.687 0.703 0.48668
사료4 6.700 6.687 1.002 0.32307
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 14.95 on 36 degrees of freedom
Multiple R-squared: 0.23, Adjusted R-squared: 0.1658
F-statistic: 3.584 on 3 and 36 DF, p-value: 0.02297
선형분석에 대한 결과값 마지막에 검정통계량과 p-value 값이 나오므로 이것을 보고 판단할 수 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 90. 분산분석 - 다중비교(Multiple Comparison) (1) | 2024.07.05 |
|---|---|
| 89. 분산분석 - 등분산성 (0) | 2024.07.04 |
| 87. 분산분석 - 변동분해 (1) | 2024.07.02 |
| 85. 일원배치 분산분석(One-Way ANOVA) (1) | 2024.06.28 |
| 84. 분산분석 통계모형(Model) (0) | 2024.06.27 |




