| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- version 2
- 고정효과모형
- 추정
- 티스토리챌린지
- 산점도
- 에세이
- JavaScript
- 변동분해
- 해운업
- 변량효과모형
- 인공지능
- 이원배치 분산분석
- 회귀분석
- 경제학
- 반복없음
- 가설검정
- 데이터 과학
- 통계학
- r
- 정규분포
- css
- version 1
- 분산분석
- 오블완
- 혼합효과모형
- 이항분포
- 확률
- 글쓰기
- html
- 반복있음
- Today
- Total
생각 작업실 The atelier of thinking
92. R의 Dataset을 이용한 분산분석 본문
Chapter 92. R의 Dataset을 이용한 분산분석
이번회차에는 R에 내장되어 있는 데이터셋을 이용하여 일원배치 분산분석을 정리해보고자 합니다.
R에는 다양한 예제 데이터셋이 내장되어 있어 데이터 분석 연습 및 예제로 활용할 수 있습니다.
data()
내장되어 있는 데이터셋 리스트
1. Dataset 소개
chickwts는 R에 기본으로 포함된 데이터셋 중 하나입니다. 이 데이터셋은 71마리의 병아리에 대한 두 가지 다른 사료 조건에서 12일 동안의 체중을 기록한 것입니다. 데이터셋은 다음과 같이 구성되어 있습니다.
(1) weight: 병아리의 체중(그램).
(2) feed : 병아리에게 제공된 사료의 종류.
"horsebean", "casein", "linseed", "soybean", "sunflower", "meatmeal"
이 데이터셋은 데이터프레임 형식으로 제공되며, 다음과 같이 불러와 사용할 수 있습니다.
data(chickwts)
위 코드를 실행하면 `chickwts` 데이터셋이 `chickwts`라는 변수에 할당됩니다. 이제 이 데이터셋을 자유롭게 분석하고 시각화할 수 있습니다.
head(chickwts) weight feed
1 179 horsebean
2 160 horsebean
3 136 horsebean
4 227 horsebean
5 217 horsebean
6 168 horsebean
dim(chickwts)[1] 71 2
71개의 자료와 2개의 열(column)로 구성되어 있습니다.
2. 데이터 시각화
사료별로 상자그림을 그려보겠습니다.
boxplot(weight~feed,chickwts, boxwex = 0.7
,col=c("skyblue",'orange','green','pink','yellow','purple'))

그림 상으로 평균의 차이는 있을 것으로 생각됩니다.
3. 분산분석표
위 자료에 대한 분산분석표를 구하는 코드는 아래와 같습니다.
summary(aov(weight~feed,data = chickwts)) Df Sum Sq Mean Sq F value Pr(>F)
feed 5 231129 46226 15.37 5.94e-10 ***
Residuals 65 195556 3009
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
위 분산분석표에서 P-value는 5.94e-10 으로 0에 가까운 값이 나타납니다. 따라서, 귀무가설을 기각합니다. 즉, 사료에 따른 체증증가는 유의미한 차이가 있다라고 할 수 있습니다.
4. 등분산성 및 정규성
우선 선형분석을 실행합니다.
result <- lm(weight~feed,data = chickwts)
summary(result)Call:
lm(formula = weight ~ feed, data = chickwts)
Residuals:
Min 1Q Median 3Q Max
-123.909 -34.413 1.571 38.170 103.091
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 323.583 15.834 20.436 < 2e-16 ***
feedhorsebean -163.383 23.485 -6.957 2.07e-09 ***
feedlinseed -104.833 22.393 -4.682 1.49e-05 ***
feedmeatmeal -46.674 22.896 -2.039 0.045567 *
feedsoybean -77.155 21.578 -3.576 0.000665 ***
feedsunflower 5.333 22.393 0.238 0.812495
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 54.85 on 65 degrees of freedom
Multiple R-squared: 0.5417, Adjusted R-squared: 0.5064
F-statistic: 15.36 on 5 and 65 DF, p-value: 5.936e-10
(1) 잔차 검진
잔차그림을 통하여 등분산성에 대한 확인을 해봅니다.
#각 수준의 잔차
resid <- residuals(result) # result$residuals
# 각 수준의 평균
yhat <- fitted(result) # result$fitted.values
# 잔차그림
plot(yhat,resid,xlab=expression(hat(y)),ylab="e",col="navy")
abline(h=0)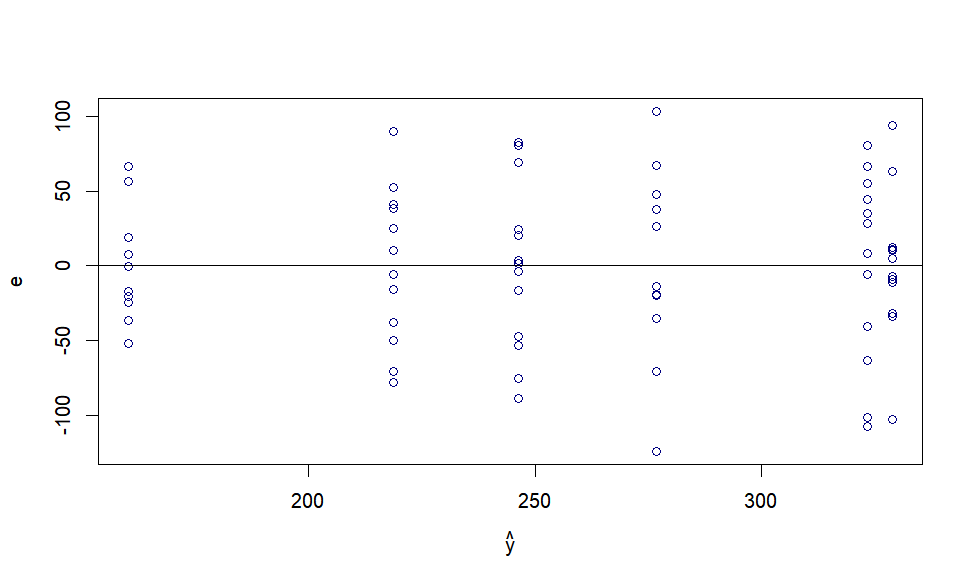
그림상으로는 등분산성을 이루는 것으로 보입니다.
(2) 등분산성- bartlett.test
bartlett.test를 이용하여 수치로 등분산성을 확인해보겠습니다.
bartlett.test(weight~feed,data=chickwts) Bartlett test of homogeneity of variances
data: weight by feed
Bartlett's K-squared = 3.2597, df = 5, p-value = 0.66
P-value는 0.66 으로 귀무가설을 기각하지 못합니다. 즉, 등분산성이 있음을 확인할 수 있습니다.
(3) 정규성 - shapiro.test
shapiro.test(resid)
Shapiro-Wilk normality test
data: resid
W = 0.98616, p-value = 0.6272
P-value는 0.6272 으로 귀무가설을 기각하지 못합니다. 즉, 정규성이 있음을 확인할 수 있습니다.
위 데이터는 등분산성과 정규성을 이루고 있음을 알 수 있습니다.
5. 다중비교
(1) Fisher's LSD
with(chickwts,pairwise.t.test(weight,feed,p.adj="none"))
Pairwise comparisons using t tests with pooled SD
data: weight and feed
casein horsebean linseed meatmeal soybean
horsebean 2.1e-09 - - - -
linseed 1.5e-05 0.01522 - - -
meatmeal 0.04557 7.5e-06 0.01348 - -
soybean 0.00067 0.00032 0.20414 0.17255 -
sunflower 0.81249 8.2e-10 6.2e-06 0.02644 0.00030
P value adjustment method: none
(2) Bonferroni
with(chickwts,pairwise.t.test(weight,feed,p.adj="bonf"))
Pairwise comparisons using t tests with pooled SD
data: weight and feed
casein horsebean linseed meatmeal soybean
horsebean 3.1e-08 - - - -
linseed 0.00022 0.22833 - - -
meatmeal 0.68350 0.00011 0.20218 - -
soybean 0.00998 0.00487 1.00000 1.00000 -
sunflower 1.00000 1.2e-08 9.3e-05 0.39653 0.00447
P value adjustment method: bonferroni
위 두 가지 방법으로 검토한 결과로,
(horsebean),(linseed,soybean),(meatmeal,casein,sunflower) 대략 3부류로 나뉜 것으로 보입니다.
6. 선형대비
사료의 종류를 동물성 사료와 식물성 사료로 나누면,
동물성 사료에는 "casein" , "meatmeal"
식물성 사료는"horsebean", , "linseed", "soybean", "sunflower" 로 분류해서 선형대비를 해보겠습니다.
library(contrast)
contrast(result, list(feed = "casein"),
list(feed = c("sunflower", "soybean","linseed", "horsebean")), type = "average")lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 85.00952 17.72813 49.60401 120.415 4.8 65 0
contrast(result, list(feed = "meatmeal"),
list(feed = c("sunflower", "soybean","linseed", "horsebean")), type = "average")
lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 38.33528 18.3597 1.668431 75.00213 2.09 65 0.0407
동물성 사료와 식물성 사료 사이에 차이가 있음을 알 수 있습니다.
하지만, sunflower와 soybean과 동물성 사료와 비교해보면,
contrast(result, list(feed = c("casein", "meatmeal")),
list(feed = c("sunflower", "soybean")), type = "average")
lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 12.57359 15.73076 -18.84291 43.99009 0.8 65 0.427
차이가 없음을 알 수 있습니다. 따라서, 보다 세부적인 원인을 찾아볼 필요가 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 94. 반복이 없는 이원배치 분산분석 I (1) | 2024.07.10 |
|---|---|
| 93. 이원배치 분산분석(Two-Way ANOVA) (0) | 2024.07.09 |
| 91. 분산분석 - 선형대비(Linear Contrast) (0) | 2024.07.07 |
| 90. 분산분석 - 다중비교(Multiple Comparison) (1) | 2024.07.05 |
| 89. 분산분석 - 등분산성 (0) | 2024.07.04 |




