| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 변동분해
- css
- version 2
- 이원배치 분산분석
- 혼합효과모형
- 반복있음
- 글쓰기
- 정규분포
- r
- version 1
- 변량효과모형
- 통계학
- 확률
- 반복없음
- html
- 이항분포
- JavaScript
- 인공지능
- 해운업
- 오블완
- 데이터 과학
- 분산분석
- 산점도
- 추정
- 티스토리챌린지
- 경제학
- 회귀분석
- 고정효과모형
- 가설검정
- 에세이
- Today
- Total
생각 작업실 The atelier of thinking
91. 분산분석 - 선형대비(Linear Contrast) 본문
Chapter 91. 분산분석 - 선형대비(Linear Contrast)
1. 선형대비(Linear Contrast)
분산분석(ANOVA)에서 선형 대비(Linear Contrast)는 다른 처리 수준의 평균 간에 특정 선형 패턴이 존재하는지를 검정하는 방법입니다. 이는 그룹 간 평균의 비교를 위해 설계된 특수한 비교 방법 중 하나입니다.
선형 대비를 사용하면 처리 간 선형적인 추세 또는 패턴이 있는지 확인할 수 있습니다. 예를 들어, 처리 간의 순서 또는 그룹 간의 등간격 차이를 평가할 수 있습니다.
일반적으로 선형 대비는 연구자가 사전에 설정한 가설을 검증하기 위해 사용됩니다. 이 방법은 사전에 계획된 비교로, 특정 가설을 테스트하기 위해 연구자가 특정 그룹 간의 평균 차이를 예상하는 경우 유용합니다.
선형 대비의 결과는 특정 가설에 대한 검정 통계량과 그에 따른 유의성을 나타내며, 이를 통해 특정 처리 간의 평균 차이에 대한 추론을 할 수 있습니다. 그러나 선형 대비를 수행하기 전에 선형성 가정을 충족하는지 확인해야 합니다. 만약 가정이 충족되지 않으면 다른 비교 방법을 고려해야 합니다.
(1) 선형대비가 필요한 상황
▶ 분산분석 결과가 귀무가설을 기각시키는 경우
분산분석 결과가 귀무가설을 기각시키지 못하는 경우에는 처리 간에 차이가 없다는 것이므로 추가분석이 필요하지 않습니다.
따라서 귀무가설을 기각시키는 경우 추가로 차이 원인을 찾아볼 필요가 있습니다.
이 때, 선형대비는 처리 효과가 어디서 발생하는지를 파악하는 데 사용됩니다. 이는 다수의 처리 그룹 간에 일정한 선형적인 패턴이 있는지를 확인하기 위한 통계적 비교 방법입니다. 처리 그룹의 평균을 비교하여 특정 처리 그룹 간의 차이가 있는지를 확인하고, 어떤 처리 그룹이 다른 처리 그룹과 유의미한 차이를 보이는지를 확인하는 데에 사용됩니다. 이를 통해 어떤 조건이나 처리가 효과적인지를 파악할 수 있습니다.
(2) 선형처리와 다중비교의 상관관계
다중 비교와 선형 대비는 서로 다른 목적과 방법을 갖고 있기 때문에 직접적인 상관 관계는 없습니다.
- 다중 비교는 여러 그룹 간의 평균을 비교하여 차이가 있는지를 확인하는 것입니다.
- 선형 대비는 특정한 처리 조건이 다른 처리 조건에 비해 어떤 영향을 미치는지를 확인하는 것입니다.
하지만 때때로 선형 대비는 특정한 그룹 간의 평균 차이를 비교하는 데 사용될 수 있습니다. 이런 경우에는 선형 대비가 다중 비교의 일부분이 될 수 있습니다. 따라서 특정 상황에서는 두 분석 방법이 연관될 수 있지만, 일반적으로는 다른 목적과 사용 방법을 갖고 있습니다.
(3) 선형대비의 통계적 특성
선형 대비는 그룹의 평균을 일렬로 늘어놓은 형태의 가중치로 이루어진 선형 결합으로 표현됩니다.
$$\mu_L = c_1\mu_1+c_2\mu_2+... + c_p\mu_p, \quad \quad \sum c_i = 0$$
즉, 계수들의 합이 0인 평균들의 선형결합이라 할 수 있습니다.
이 때, 모평균은 가중치를 가진 표본평균의 합으로 추정합니다.
$$\mu_i \impliedby \bar{Y_i}$$
$$ L = c-1\bar{Y_1}+c_2\bar{Y_2}+...+c_p\bar{Y_p}$$
추정량 L 은 아래와 같은 정규분포를 따릅니다.
$$L \sim N(\mu_L, \sigma_L^2)$$
이 때 모분산은 아래와 같이 정리할 수 있습니다.
$$\sigma_L^2 = Var(c_1\bar{Y_1}+c_2\bar{Y_2}+...+c_p\bar{Y_p})$$
$$= \sigma^2 \sum c_i^2/n_i $$
이 때 모분산 α2 을 알 수 없으므로 추정량은 MSE를 사용합니다.
$\sigma_L^2$의 추정량 : $S_L^2 = MSE \sum c_i^2 / n_i $
(4) 중심축량
표준화를 하면,
$$ \frac{L - \mu_L}{S_L}$$
위 추정량을 대입하여 정리하면,
$$T = \frac{L - \mu_L}{S_L} = \frac{L - \mu_L}{\sqrt{MSE} \sqrt{\sum C_i^2/n_i}} \sim t_{N-p}$$
중심축량은 자유도 N-P 인 t 분포를 따릅니다.
2. 선형대비 가설 검정
◈ 예제 : 4가지 사료에 따른 체중증가 실험
| 방법 | 쇠고기 저단백 |
쇠고기 고단백 |
시리얼 저단백 |
시리얼 고단백 |
| 반복 | 90 76 90 64 86 51 72 90 95 78 |
73 102 118 104 81 107 100 87 117 111 |
107 95 97 80 98 74 74 67 89 58 |
98 74 56 111 95 88 82 77 86 92 |
| 합 | 792 | 1000 | 839 | 859 |
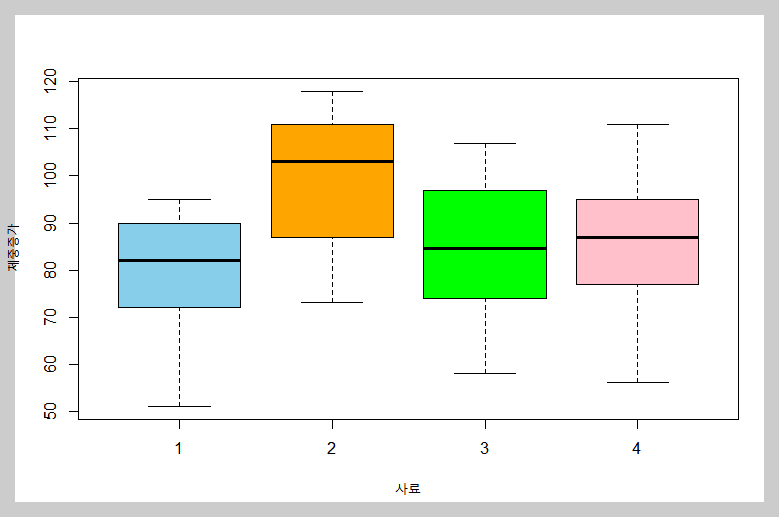
분산분석표는 아래와 같습니다.
summary(aov(체중증가~사료,data=rats)) Df Sum Sq Mean Sq F value Pr(>F)
사료 3 2404 801.4 3.584 0.023 *
Residuals 36 8049 223.6
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
P-value가 0.023으로 5% 유의수준보다 작으므로 처리효과가 있다고 할 수 있습니다.
위 예제에 대한 선형대비 가설검정을 해보겠습니다.
(1) 가설 설정
우선 귀무가설은 차이가 없다는 것으로 설정합니다. 따라서, 일반화된 귀무가설은 아래와 같습니다.
$$H_0 : \mu_L = c_1\mu_1+c_2\mu_2+... + c_p\mu_p = 0$$
위 예제에서의 귀무가설은 조건에 따라 달리 설정할 수 있습니다.
위 예제에서 처리효과의 원인을 아래의 3가지 경우로 찾아보려고 한다면, 각각의 귀무가설은 ,
① 단백질 원료(Beef, Cereal)에 따른 차이
$$H_0 : \mu_1+\mu_2 = \mu_3+\mu_4 $$
$$ \implies \mu_1+\mu_2 - \mu_3 - \mu_4 = 0 $$
Beef는 사료 1,2 , Cereal은 사료 3,4 간 차이가 없다는 것이 귀무가설이 됩니다.
② 단백질 양(Low, High)에 따른 차이
$$H_0 : \mu_1+\mu_3 = \mu_2+\mu_4 $$
$$ \implies \mu_1-\mu_2 + \mu_3 - \mu_4 = 0 $$
단백질 양 Low 는 사료 1,3 , High는 사료 2,4 간 차이가 없다는 것이 귀무가설이 됩니다.
③ 사료1은 A 제조사, 2,3,4는 B 제조사 일 때, 제조사 간의 차이
$$H_0 : \mu_1 = \frac{\mu_2+\mu_3+\mu_4}{3}$$
$$ \implies 3 \mu_1 - \mu_2 - \mu_3 - \mu_4 = 0$$
제조사 A 는 사료 1 제조사 B는 사료 2,3,4 간 차이가 없다는 것이 귀무가설이 됩니다.
(2) 검정 통계량
앞에서 검정통계량은 아래와 같이 얻었습니다.
$$T = \frac{L}{S_L} = \frac{L}{\sqrt{MSE} \sqrt{\sum C_i^2/n_i}} \sim t_{N-p}$$
이 검정통계량을 제곱하면 아래와 같습니다.
$$T^2 = \frac{L^2}{MSE \sum C_i^2/n_i \sim F_{1,N-p}$$
제곱한 검정통계량은 여러모로 계산상 편의가 있습니다. 또한 F 분포를 따릅니다.
검정통계량은 이 제곱한 검정통계량을 사용합니다.
이제 위 예제의 각 경우에서 검정통계량을 구해보면, 아래와 같습니다.
먼저, 위 예제 분산분석표에서 MSE는 223.6 임을 알 수 있습니다.
① 단백질 원료(Beef, Cereal)에 따른 차이
$$L = 9.4, \quad S_L^2 = \frac{223.59}{10}(1^2+1^2+(-1)^2)+(-1)^2) = 89.436$$
$$t_0^2 = \frac{9.4^2}{89.436}=0.988 < 4.113 = F_{0.05, 1, 36}$$
⇒ 검정통계량은 채택역에 있습니다. 따라서, 귀무가설을 기각할 수 없습니다. 즉 단백질 원료에 따른 차이는 없다고 할 수 있습니다.
② 단백질 양(Low, High)에 따른 차이
$$L = -22.8, \quad S_L^2 = \frac{223.59}{10}(1^2+1^2+(-1)^2)+(-1)^2) = 89.436$$
$$t_0^2 = \frac{(-22.8)^2}{89.436}= 5.812 > 4.113 = F_{0.05, 1, 36}$$
⇒ 검정통계량은 기각역에 있습니다. 따라서, 귀무가설을 기각할 수 있습니다. 즉 단백질 양에 따른 차이가 있다고 할 수 있습니다.
③ 사료1은 A 제조사, 2,3,4는 B 제조사 일 때, 제조사 간의 차이
$$L = -32.2, \quad S_L^2 = \frac{223.59}{10}(3^2+(-1)^2+(-1)^2)+(-1)^2) = 268.308$$
$$t_0^2 = \frac{(-32.2)^2}{268.308}=3.864 < 4.113 = F_{0.05, 1, 36}$$
⇒ 검정통계량은 채택역에 있습니다. 따라서, 귀무가설을 기각할 수 없습니다. 즉 제조사에 따른 차이는 없다고 할 수 있습니다.
위 예제에서 유의미한 차이는 ② 단백질 양(Low, High)에 따른 차이에서 발생하였습니다.
3. R을 이용한 선형대비
Contrast 패키지는 R에서 다중비교 및 대조분석을 수행하는 데 사용되는 도구를 제공하는 패키지입니다. 이 패키지는 다양한 유형의 다중비교를 수행하는 함수와 대조분석을 위한 함수를 포함하고 있습니다.
# Linear Contrast
install.packages("contrast")
library(contrast)
① 단백질 원료(Beef, Cereal)에 따른 차이
rats <- read.csv("rats.csv",header = TRUE, fileEncoding = "CP949",
encoding = "UTF-8")
rats$사료 <- as.factor(rats$사료)
result <- lm(체중증가~사료,data=rats)
contrast(result,list(사료=c("1","2")),list(사료=c("3","4")),type="average")
lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 4.7 4.728577 -4.89 14.29 0.99 36 0.3269
- Contrast: 대조 값
- S.E.: 표준 오차 (Standard Error)
- Lower: 신뢰 구간의 하한 (Confidence Interval Lower Bound)
- Upper: 신뢰 구간의 상한 (Confidence Interval Upper Bound)
- t: t-통계량 (t-Statistic)
- df: 자유도 (Degrees of Freedom)
- Pr(>|t|): p-값 (p-Value)
contrast( ) 함수는 t 검정을 사용합니다. 선형모델을 사용합니다.
위 결과값은 p-value 0.3269로 귀무가설을 기각하지 못합니다.
② 단백질 양(Low, High)에 따른 차이
contrast(result,list(사료=c("1","3")),list(사료=c("2","4")),type="average")
lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 -11.4 4.728577 -20.99 -1.81 -2.41 36 0.0211
위 결과값은 p-value 0.0211로 5% 유의수준에서 귀무가설을 기각할 수 있습니다.
③ 사료1은 A 제조사, 2,3,4는 B 제조사 일 때, 제조사 간의 차이
contrast(result,list(사료="1"),list(사료=c("2","3","4")),type="average")lm model parameter contrast
Contrast S.E. Lower Upper t df Pr(>|t|)
1 -10.73333 5.460091 -21.80691 0.3402443 -1.97 36 0.0571
위 결과값은 p-value 0.0571로 5% 유의수준에서 귀무가설을 기각할 수 없습니다.
'통계학 이야기' 카테고리의 다른 글
| 93. 이원배치 분산분석(Two-Way ANOVA) (0) | 2024.07.09 |
|---|---|
| 92. R의 Dataset을 이용한 분산분석 (0) | 2024.07.08 |
| 90. 분산분석 - 다중비교(Multiple Comparison) (1) | 2024.07.05 |
| 89. 분산분석 - 등분산성 (0) | 2024.07.04 |
| 88. R을 이용한 분산분석(ANOVA) (1) | 2024.07.03 |




