| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 이원배치 분산분석
- 추정
- 에세이
- 반복있음
- 변동분해
- 통계학
- 혼합효과모형
- 회귀분석
- r
- 변량효과모형
- 오블완
- 티스토리챌린지
- 정규분포
- 인공지능
- 반복없음
- 확률
- 이항분포
- 가설검정
- 해운업
- 산점도
- 경제학
- html
- css
- 데이터 과학
- 글쓰기
- version 1
- version 2
- JavaScript
- 분산분석
- 고정효과모형
- Today
- Total
생각 작업실 The atelier of thinking
44. 초기하 분포(Hypergeometric Distribution) - 이산확률분포 본문
Chapter 44. 초기하분포(Hypergeometric Distribution)
1. 초기하분포 (Hypergeometric Distribution)의 정의
초기하분포는 이항분포와 비슷한 분포이지만, 복원추출이 아닌 비복원추출에서의 확률분포입니다.
유한모집단이 두 그룹으로 나누어져 있고 표본을 비복원으로 추출할 때, 특정 그룹에서 뽑힌 표본의 수에 대한 확률분포입니다. 이항분포에서 성공과 실패 두 그룹에서 뽑는 것은 같지만, 비복원추출이고 각 시행은 독립이 아니라는 점에 차이가 있습니다.
2. 초기하분포 확률변수
크기가 N인 모집단이 크기가 M과 N-M인 두 개의 부모집단 (A,B)로 나누어진 경우,
n개의 표본을 비복원으로 추출할 때, 부모집단(A)에서 추출될 표본의 수가 확률변수 입니다.
A에서 추출되면 1, 다른집단에서 추출되면 0 으로 표시합니다. 즉, n개의 합이 A에서 추출될 표본의 수가 되고, 이것이 확률변수입니다.
확률변수는 이항분포와 같지만, 추출과정은 독립적이지 않다는 것이 차이점입니다.
3. 초기하 분포 확률질량함수
확률질량함수를 아래의 예제로 부터 유도해보겠습니다.
◈ 예제 : 6개가 정상품과 4개의 불량품이 있는 상자에서 임의로 3개의 제품을 비복원 추출한 경우에
3개 중 1개가 불량품일 확률은 ?

3개 중 1개가 불량품일 사건은 { (불량,정상,정상), (정상,불량,정상),(정상,정상,불량) } 으로 나타납니다.
각각의 확률을 구하면,
P(불량,정상,정상)=410×69×58
P(정상,불량,정상)=610×49×58
P(정상,정상,불량)=610×59×48
세 확률을 더하면 3개 중 1개가 불량품인 사건의 확률을 구할 수 있습니다.
위 각 확률은 분자는 4 X 5 X 6, 분모는 10 X 9 X 8 이므로 아래와 같이 표현할 수 있습니다.
3×6×5×410×9×8=12
위 식을 분리해서 하나씩 살펴보면,
앞의 3은 위치 중 하나를 선택해 "불량"을 대입하는 것입니다. 이는 조합공식을 이용해 구할 수 있습니다.
\dbinom{3}{1} = \frac{3!}{1!(3-1)!} = 3
분자를 이루는 4는 불량품 4개에서 1개를 비복원 추출나열하는 방법으로 순열공식을 이용해 구할 수 있습니다.
\frac{4!}{(4-1)!} = 4
분자를 이루는 6 X 5 는 정상품 6개에서 2개를 비복원 추출 나열하는 방법으로 이것도 순열공식을 이용해 구할 수 있습니다.
\frac{6!}{(6-2)!} = 6 \times 5
분모는 10개에서 3개를 비복원 추출 나열하는 방법으로 아래와 같이 표현할 수 있습니다.
\frac{10!}{(10-3)!} = 10 \times 9 \times 8
확률 계산식에 이를 적용하면, 아래와 같이 나타낼 수 있습니다.
P(X=1) = \frac{3!}{1!(3-1)!} \frac { \frac{4!}{(4-1)!} \frac{6!}{(6-2)!}} { \frac{10!}{(10-3)!}}
\frac {3!}{1!(3-1)!} 를 정리하면 아래와 같습니다.
P(X=1) = \frac{\frac{4!}{1!(4-1)!} \frac{6!}{2!(6-2)!}}{\frac{10!}{3!(10-3)!}}
이 식은 각각의 조합이 됩니다. 따라서 아래와 같이 표현할 수 있습니다.
P(X=1) = \frac{ \dbinom{4}{1} \dbinom{6}{2} }{ \dbinom{10}{3}}
이를 확률질량함수로 나타내면, 아래와 같습니다.
f(x) = \frac{ \dbinom{4}{x} \dbinom{6}{3-x} }{ \dbinom{10}{3}}, x=0,1,2,3
이제 확률질량함수 일반식으로 표현한다면,
모집단 크기 : N , M과 N-M인 두 개의 부모집단, n : 추출될 표본의 수
f(x) = \frac{ \dbinom{M}{x} \dbinom{N-M}{n-x} }{ \dbinom{N}{n}}, x=0,1,2,..,n
단, x는 특정집단의 수보다 많아서는 안됩니다. 위 예제에서 불량품의 총 수는 4개인 데 5개의 불량품을 뽑는 확률은 구할 수 없기 때문입니다. 또한 음수의 값을 갖을 수 없습니다. 그런 의미로
x= max(0,n-N+M), ..., min(n,M)
으로 표기하기도 합니다. 대부분의 경우는 0 부터 n까지로 표기해도 무방합니다.
4. 초기화 확률변수의 기대값과 분산
(1) 기대값
초기하 확률변수의 기대값은 각 시행에서 A집단에서 추출되면 1, 다른 집단에서 추출되면 0으로 표시한 베르누이 확률변수의 합으로 표현됩니다.
X_1+X_2+ ... + X_n = X
A 1 1 ... 1 ↓
B 0 0 ... 0 A에서 추출된 표본의 수
N 모집단의 크기를 N이라 하고 A집단의 크기 M 이라 할 때, X_i를 뽑을 확률은 \frac{M}{N}이 됩니다.
비복원 추출이라 하더라도 추출한 이후의 확률이 바뀌는 것이지 앞의 확률을 모를 때에는 모든 확률은 동일하다고 할 수 있습니다.
따라서 기대값은 아래와 같이 표현할 수 있습니다.
E(X_i) = \frac{M}{N} = p
E(X) = n \frac{M}{N} = np
이항분포에서와 같은 결과가 나옵니다.
(2) 분산
Var(X_i) = E(X_i^2) - E(X_i)^2
E(X_i^2) = p
Var(X_i) = p - p^2 = p(1-p) = \frac{M}{N} \frac{N-M}{N}
초기하분포가 이항분포와 다른 점은 비복원이므로 각각의 시행이 독립이 아닙니다.
독립이 아니면 공분산이 0 이 아닙니다.
Var(X+Y) = Var(X) + Var(Y) + 2Cov(X,Y) 을 적용하면,
Var(X)=Var(X_1+X_2+...+X_n) = \sum_{i} Var(X_i) + 2\sum_{i<j} Cov(X_i,X_j)
공분산을 따로 살펴보면,
\sum{i<j} 의 의미는 공분산의 갯수는 n개에서 서로다른 2개를 조합한 것이라 볼 수 있습니다.
즉, \sum{i<j} 는 \dbinom{n}{2} = \frac{n!}{2!(n-2)!} 로 구할 수 있습니다.
공분산은 아래의 공식으로 구할 수 있습니다.
Cov(X_i,X_j) = E(X_i X_j) - E(X_i)E(X_j)
X_i 나 X_j는 0 또는 1 의 값을 가지고 있습니다. 값이 0이 하나라도 있으면 0이 되기 때문에 X_i가 1이고 X_j가 1일 때 확률만 구하면 됩니다.
E(X_iX_j) = P(X_i=1, X_j=1) = P(X_i=1)P(X_j=1|X_i =1)
P(X_i=1) = \frac{M}{N}
P(X_j=1|X_i=1)= \frac{M-1}{N-1}
X_i을 실행한 후이므로 각각 1 씩 감소하게 됩니다.
위 내용을 정리하면,
E(X_i,X_j) = \frac{M}{N} \frac{M-1}{N-1} , E(X_i)= E(X_j) = \frac{M}{N}
이제 공분산을 구하는 식은 Cov(X_i,X_j) = E(X_i X_j) - E(X_i)E(X_j) = \frac{M}{N} \frac{M-1}{N-1} - ( \frac{M}{N})^2 위 식을 풀어 정리하면, = \frac{M}{N}(\frac{M-1}{N-1} - \frac{M}{N} ) = \frac{M}{N}(\frac{NM-N-MN+M}{N(N-1)}) = - \frac{M}{N}(\frac{N-M}{N(N-1)} = \frac{M}{N} ( \frac{1-\frac{M}{N}}{N-1})
위 식에 \frac{M}{N} = p 로 바꾸면,
Cov(X_i,X_j) = - \frac{p(1-p)}{N-1}
이제 분산 Var(X) 를 구하는 아래 식에 각각 구한 것을 대입해 보겠습니다.
Var(X)=Var(X_1+X_2+...+X_n) = \sum_{i} Var(X_i) + 2\sum_{i<j} Cov(X_i,X_j)
\sum_{i} Var(X_i) = np(1-p) , 2 \sum_{i<j} = 2 \dbinom{n}{2} = 2 \frac{n!}{2!(n-2)!} = n(n-1)
Cov(X_i,X_j) = - \frac{p(1-p)}{N-1}
Var(X) = np(1-p) - n(n-1) \frac{p(1-p)}{N-1} = np(1-p)(1-\frac{N-n}{N-1})
위 분산식에서 \frac{N-n}{N-1} 을 유한모집단 수정계수라 부릅니다. 이 계수는 1보다 작습니다.
앞서 이항분포의 분산은 np(1-p) 로 나타납니다. 반면 초기하분포의 분산은 np(1-p) 에 1-수정계수를 곱한값입니다.
Var(X) = np(1-p)(1-\frac{N-n}{N-1})
이는 초기하분포의 분산이 이항분포의 분산보다 작다는 것을 의미합니다.
분산은 퍼져있는 정도를 나타내는 데 분산이 작다는 것은 변동성이 적다는 의미입니다. 그만큼 안정적인 셩채라고 볼 수 있습니다. 따라서 초기하분포가 이항분포보다 좀 더 좋은 성질을 가지고 있다는 의미입니다.
다만 초기하분포는 이항분포에 비해 다루기가 조금 어렵다보니 이항분포로 설명하는 경우가 많을 뿐입니다.
5. 초기하분포 vs 이항분포
| 초기하분포 | 이항분포 | |
| 확률변수 | X = X_1+X_2+ ... + X_n | X = X_1+X_2+ ... + X_n |
| 확률질량함수 f(x) | \frac{ \dbinom{M}{x} \dbinom{N-M}{n-x} }{ \dbinom{N}{n}}, x=0,1,2,..,n | \dbinom{n}{x} p^x(1-p)^{n-x} , x = 0,1,2,...,n |
| 확률분포 표시 | X \backsim HYP(N,K,n) | X \backsim B(n,p) |
| 기대값 E(X) | np | np |
| 분산 Var(X) | np(1-p)(1-\frac{N-n}{N-1}) | np(1-p) |
| 표준편차 SD(X) | \sqrt {p(1-p)(1-\frac{N-n}{N-1})} | \sqrt {np(1-p)} |
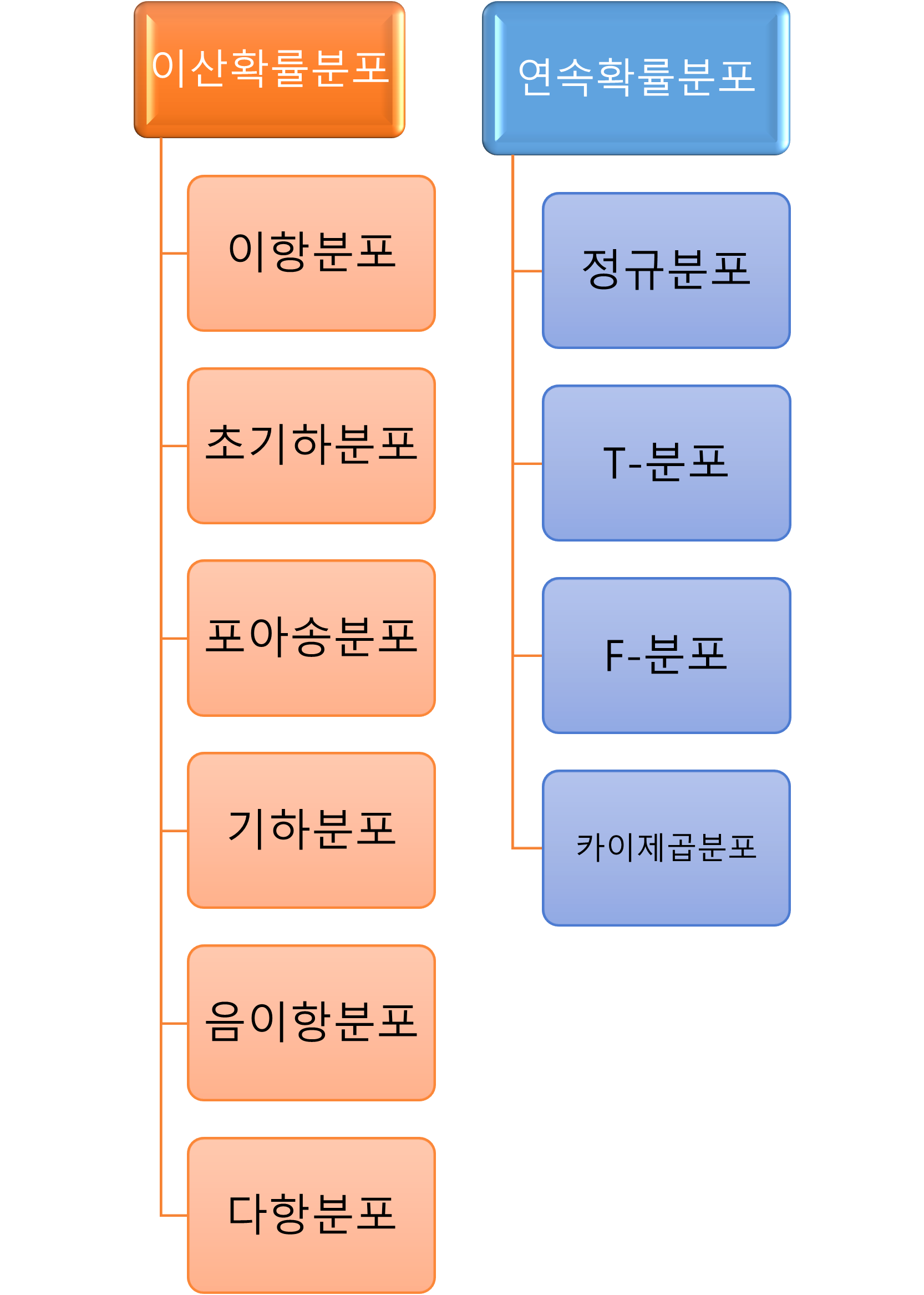
확률분포의 분류
'통계학 이야기' 카테고리의 다른 글
| 46. 포아송분포(Poisson Distribution) - 이산확률분포 (1) | 2023.10.27 |
|---|---|
| 45. R을 이용한 확률분포 - 초기하분포 구하기 (1) | 2023.10.26 |
| 43. R을 이용한 확률분포 - 이항분포 구하기 (0) | 2023.10.25 |
| 42. 베르누이분포 & 이항분포 (이산확률분포) (0) | 2023.10.24 |
| 41. 확률분포의 분류 (1) | 2023.10.23 |




