생각 작업실 The atelier of thinking
46. 포아송분포(Poisson Distribution) - 이산확률분포 본문
Chapter 45. 포아송분포(Poisson Distribution)
1. 포아송분포(Poisson Distribution)의 정의
포아송분포는 단위시간 동안 혹은 단위공간에서 어떤 사건이 발생하는 횟수를 나타내는 이산확률분포입니다.
포아송분포는 사건발생률이 일정하고 독립적으로 발생하는 경우에 적용됩니다. 주로 사건 발생에 대한 희귀한 사건을 모델링하는 데 사용됩니다. 예를 들어 단위 시간당 발생하는 교통사고 수, 단위 면적당 나타나는 군락의 개수, 자연재해의 발생률 등을 모델링할 때 사용됩니다.
2. 포아송분포 확률변수
포아송분포의 확률변수는 일정한 시간, 공간 또는 구간에서 발생하는 사건의 수를 나타내는데 사용됩니다.
이 확률변수를 일반적으로 "X"로 표기합니다.
포아송 분포는 다음과 같이 표현합니다.
$$ X \backsim Pois(\lambda) $$
포아송 분포에서 확률변수 X는 정수값을 취하며, 주어진 구간 또는 시간 동안의 평균 사건 발생횟수를 나타냅니다.
3. 포아송분포 확률질량함수
발생 가능성이 희박한 사건이 임의의 구간에서 평균적으로 $\lambda$ 번 발생한다고 했을 때에 전제조건은,
구간을 나누었을 때 각 구간의 발생빈도는 서로 독립 (independent increment) 이어야하고,
구간의 위치와 관계없이 동일 길이의 구간에서의 평균 발생 빈도는 동일(staionary increment)해야 한다는 것입니다.
확률변수 X는 위 상황에서 해당 사건이 일어날 횟수입니다.
포아송분포는,
$$ X \backsim Pois(\lambda) $$
이를 나타내는 확률질량함수는 다음과 같습니다.
$$ f(x) = \frac{e^{- \lambda} \lambda^x}{x!} , x = 0,1,2,... $$
4. 포아송 확률변수의 기대값과 분산
포아송분포는 기대값과 분산이 같다는 특징이 있습니다.
포아송 분포의 확률변수 X의 기대값과 분산은 모두 $\lambda$ 로 같습니다.
포아송분포의 기대값은
$$ E(X) = \lambda $$
포아송분포의 분산은,
$$ Var(X) = \lambda $$
여기서 $\lambda$는 포아송분포의 모수로 평균적으로 발생하는 사건의 수를 나타내며, 기대값과 분산이 같다는 특징은 포아송분포를 특별하게 만드는 특성 중 하나입니다. 이것은 포아송분포가 사건발생률이 일정하고, 사건들이 서로 독립적으로 발생할 때 주로 발생하는 확률분포 중 하나이기 때문입니다.
5. 이항분포와 포아송분포
이항분포 $B \backsim (n,p) $ 에서 n이 커지면 계산하는데 어려움이 있습니다.
또한 p가 매우 작으면 큰 x에 대한 확률은 무시할 정도로 작게 나타납니다.예를 들어 $B \backsim (n,p) , n= 1000, p=0.005 $ 일 때의 그래프를 보면,
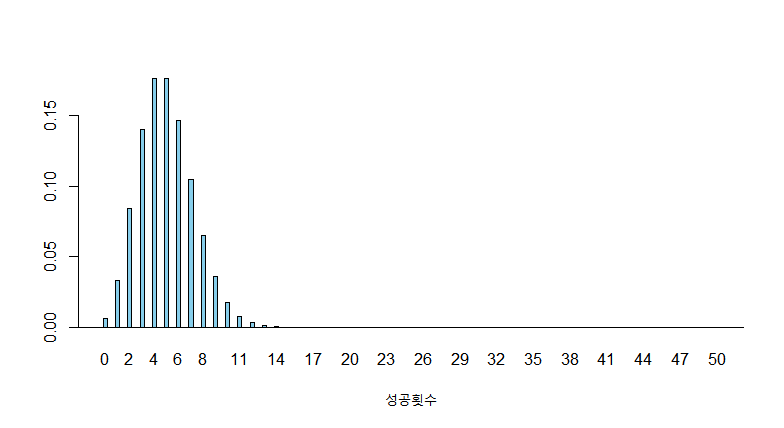
위 그래프를 보면 x가 15이상이면 0에 가깝게 나타납니다.
이항분포 중에 n이 크고 p가 작은 경우에는 포아송분포와 크게 차이가 나지 않습니다.
◈ 예제 : 반도체 생산공정
평균 500개 중 한 개 정도가 불량품이었고 무작위로 발생한다고 했을 때,
제작된 1500개 반도체 중 불량품이 2개 이하일 확률은 ?
(1) 이항분포
위 경우를 이항분포로 표현하면, $ X \backsim B(1500,1/500) $ 일 때 $ P(X \leq 2) $ ?
p = 1/500 , n = 1500 , X : 1500 개 반도체 중 불량품 수
$$ P(X \leq 2) = \sum_{x=0}^2 \binom{1500}{x}(\frac{1}{500})^x(\frac{499}{500})^{1500-x} = 0.4230 $$
(2) 포아송분포
위 경우를 포아송분포로 표현하면, $ \lambda = np = 1500 \times 1/500 = 3 $ 이므로 $ X \backsim Pois(3) $
$$ P(X \leq 2) = \sum_{x=0}^2 \frac{e^{-3} 3^x}{x!} = 0.4232 $$
※ n이 크고 p가 작은 이항분포의 경우 포아송 분포와 차이가 거의 없습니다.
$\lambda$ 가 5 이하이면 포아송 근사가 잘 이루어집니다.
6. 포아송분포의 성질
이항분포와 같은 성질을 가지고 있습니다.
이항분포 $X \backsim B(m,p) , Y \backsim B(n,p)$ 이고 X와 Y 가 독립이면, X+Y의 분포는
$ X+Y \backsim B(m+n, p) $ 형태의 이항분포가 됩니다.
포아송분포 $X \backsim Pois(\lambda_1), Y \backsim Pois(\lambda_2) $ 이고 X와 Y가 독립이면, X+Y의 분포는 $ X+Y \backsim Pois(\lambda_1+\lambda_2)$ 형태의 포아송분포가 됩니다.
7. 포아송분포 vs 이항분포
| 초기하분포 | 이항분포 | |
| 확률변수 | $ X $ | $ X = X_1+X_2+ ... + X_n $ |
| 확률질량함수 $f(x)$ | $ \frac{e^{- \lambda} \lambda^x}{x!} , x = 0,1,2,... $ | $ \dbinom{n}{x} p^x(1-p)^{n-x} , x = 0,1,2,...,n $ |
| 확률분포 표시 | $ X \backsim Pois(\lambda) $ | $ X \backsim B(n,p) $ |
| 기대값 $E(X)$ | $\lambda$ | $np$ |
| 분산 $Var(X)$ | $\lambda$ | $np(1-p)$ |
| 표준편차 $SD(X)$ | $ \sqrt {\lambda} $ | $ \sqrt {np(1-p)}$ |
확률분포의 분류

'통계학 이야기' 카테고리의 다른 글
| 48. 기하분포와 음이항분포 - 이산확률분포 (2) | 2023.10.31 |
|---|---|
| 47. R을 이용한 확률분포 - 포아송 분포 구하기 (1) | 2023.10.30 |
| 45. R을 이용한 확률분포 - 초기하분포 구하기 (1) | 2023.10.26 |
| 44. 초기하 분포(Hypergeometric Distribution) - 이산확률분포 (1) | 2023.10.26 |
| 43. R을 이용한 확률분포 - 이항분포 구하기 (0) | 2023.10.25 |




