생각 작업실 The atelier of thinking
50. 다항분포(Multinomial Distribution) - 이산확률분포 본문
Chapter 50. 다항분포(Multinomial Distribution)
1. 다항분포의 정의
다항분포는 여러 개의 값을 가질 수 있는 독립확률변수들에 대한 확률분포로, 여러 번의 독립적 시행에서 각각의 값이 특정 횟수가 나타날 확률을 정의합니다.
이항분포의 확장된 형태라고 할 수 있습니다. 다항분포에서 차원이 2인 경우는 이항분포가 됩니다.
이항분포를 그림으로 표현하면 아래와 같습니다.

다항분포를 그림으로 표현하면 아래와 같습니다.

각 시행에서 나온 결과(S)는 k개이고 각 결과의 횟수(X)가 각각의 확률변수가 됩니다.
각 시행에서 결과의 확률(P)들의 합은 1이 됩니다.
$$ \sum_{i=1}^k p_i = 1 $$
n 번 시행했을 때, 각 결과의 횟수를 도수분포표로 나타내면,
| 시행 | 결과(S) 1 | 결과(S) 2 | ... ... | 결과(S) k | 합 |
| 1 | $X_{11}$ | $X_{12}$ | ... ... | $X_{1k}$ | 1 |
| 2 | $X_{21}$ | $X_{22}$ | ... ... | $X_{2k}$ | 1 |
| : . |
: . |
: . |
... ... : |
: . |
|
| $n$ | $X_{n1}$ | $X_{n2}$ | $X_{nk}$ | 1 | |
| 합 | $X_1$ | $X_2$ | $X_k$ | $n$ |
$X_{ij} : i$번째 시행에서 결과 $j$ 가 나오면 1 아니면 0 로 하면 각 시행마다 합은 1이 됩니다.
만약 $X_{11} $ 이 1이라면 나머지 $X_{1j}$ 는 모두 0이 됩니다.
각 시행마다는 서로 독립입니다. 즉, $i_1 \not= i_2 $ 경우를 말합니다.
2. 다항분포의 확률질량함수
다항분포는 이항분포의 확장된 형태입니다. 다항분포의 확률질량함수는 이항분포로부터 유도할 수 있습니다.
다항분포에서 각 결과값의 기준으로 본다면, 각 결과값은 이항분포를 나타냅니다.
예를 들어 결과값 $X_1$ 을 기준으로 본다면, $X_1$ 이 나오면 1, 그리고 그 이외의 것이 나오면 0으로 볼 수 있습니다. 즉 $X_1$ 만 관심을 갖는다면 이항분포라고 할 수 있습니다.
이항분포의 질량함수는 아래와 같습니다.
$ X_1 \backsim B( n, p_1 ) $
$$ f(x_1) = \frac{n!}{x_1 !(n-x_1)!} p_1^{x_1} (1-p_1)^{n-x_1} $$
위 식에서 $n-X_1 = X_2$ 로, $1-P_1 = P_2$ 로 표현하면 아래와 같이 나타납니다.
$$ f(x_1,x_2) = \frac{n!}{x_1 !x_2!} p_1^{x_1} p_2^{x_2} , x_1+x_2 = n , p_1+p_2 = 1 $$
위의 식을 확장해서 $X_3$ 를 추가한다면, 아래와 같이 나타낼 수 있습니다.
$$ f(x_1,x_2,x_3) = \frac{n!}{x_1 !x_2! x_3!} p_1^{x_1} p_2^{x_2} p_3^{x_3} , x_1+x_2+x_3=n , p_1+p_2+p_3 = 1 $$
위의 식을 k개까지 확장하면 다항분포의 확률질량함수를 구할 수 있습니다.
다항분포의 확률질량함수는 아래와 같습니다.
$$ f(x_1,x_2,..., x_k) = \frac{n!}{x_1 !x_2!... x_k!} p_1^{x_1} p_2^{x_2}... p_k^{x_k} $$
$$ \sum_{i=1}^k x_i = n , \sum_{i=1}^k p_i = 1 $$
3. 특정결과에 대한 기대값과 분산
i 번째 결과에만 관심이 있다면, 나머지 결과를 따로 묶게 되면 이항분포가 됩니다.
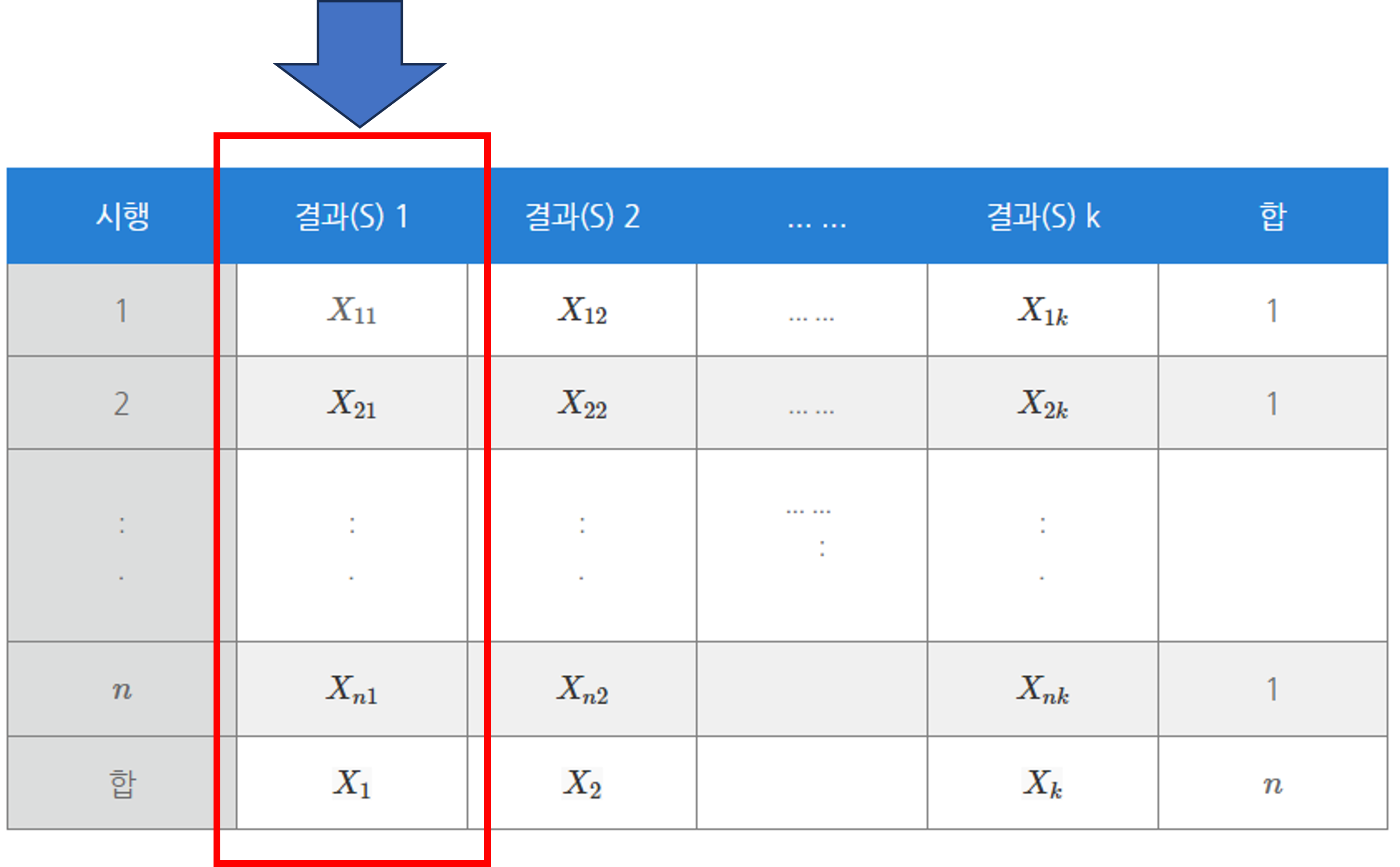
각각의 기대값과 분산은 이항분포의 기대값과 분산을 적용합니다. 따라서 아래와 같이 표현합니다.
$$ X_i \backsim B ( n, p_i ) $$
$$ E(X_i) = n p_i $$
$$ Var(X_i) = n p_i(1-p_i) $$
i 번째 또는 j 번째 결과에 관심이 있다면, 이는 두 합의 이항분포로 구할 수 있습니다.
$$ Y = X_i + X_j \backsim B( n, p_i+p_j) $$
$$ E(Y) = E(X_i+X_j) = n(p_i+p_j) $$
$$ Var(Y) = Var(X_i+X_j) = n(p_i+p_j)(1-(p_i+p_j)) $$
4. 다항분포의 공분산과 상관관계
(1) 공분산
$X_i, X_j $ 와의 관계 - 2번 실험을 하였다고 가정하면,
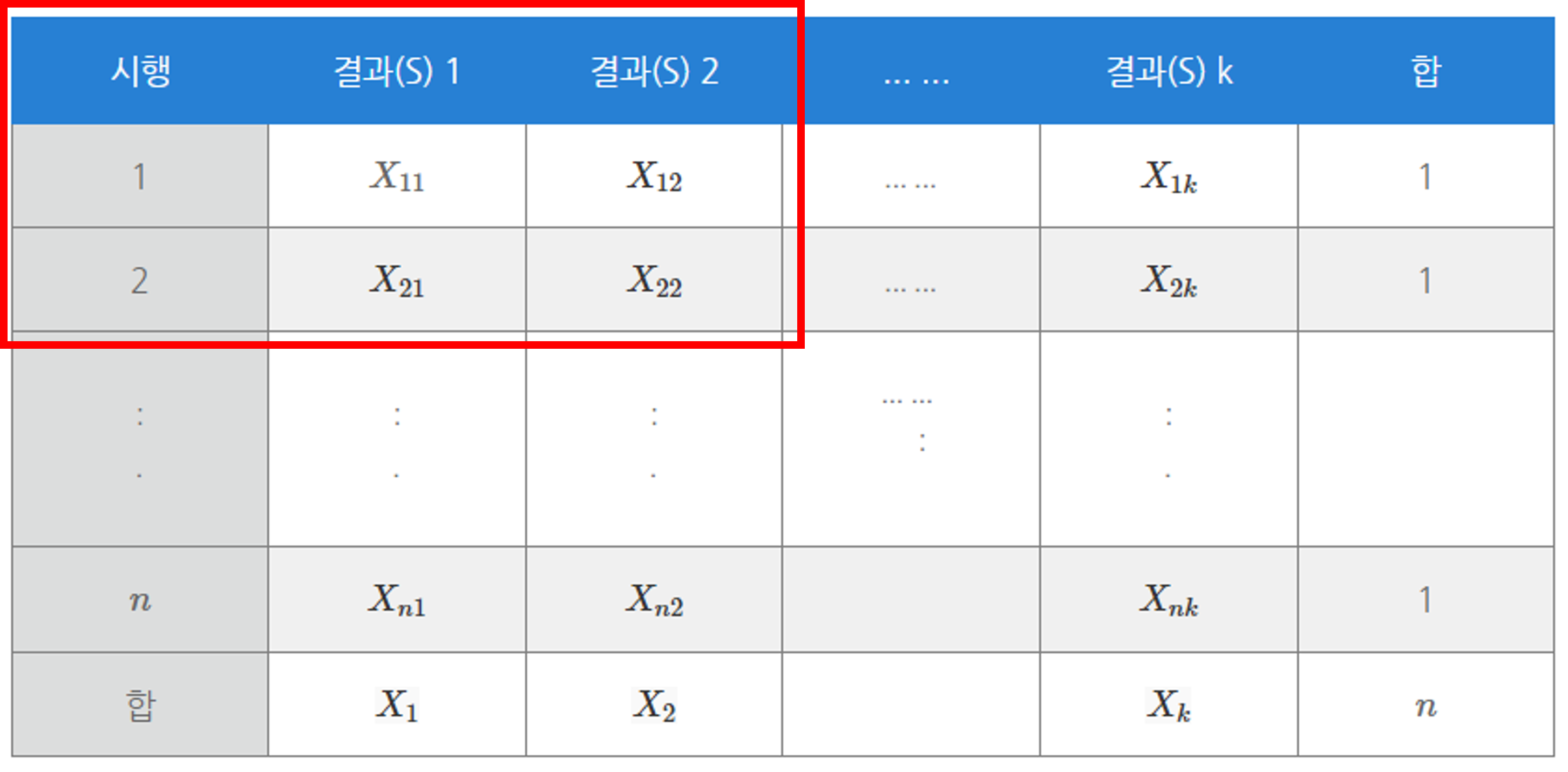
$$ X_1 = X_{11}+X_{21} , X_2 = X_{12}+X_{22} $$
$$ Cov(X_1,X_2) = Cov(X_{11}+X_{21} , X_{12}+X_{22}) $$
$$ = Cov(X_{11},X_{12})+Cov(X_{11},X_{22})+Cov(X_{21},X_{12})+Cov(X_{21},X_{22}) $$
각 시행별로는 독립이으로 공분산은 0 이 됩니다. 위에서 $ Cov(X_{11},X_{22}),Cov(X_{12},X_{21}) $ 는 0이 됩니다. 즉 같은 시행에서의 공분산만 구하면 됩니다.
따라서, 위 공분산 식은 아래와 같이 표현할 수 있습니다.
$$ Cov(X_1, X_2) = \sum_{i=1}^n Cov(X_{i1}, X_{i2}) $$
$$ Cov(X_{i1}, X_{i2}) = E(X_{i1} X_{i2}) - E(X_{i1}) E(X_{i2}) $$
$$ E(X_{ij}) = p_j , X_{i1} 과 X_{i2} 중 하나는 1 이고 나머지는 0 이므로 E(X_{i1} X_{i2}) = 0 $$
$$ → Cov(X_{i1} , X_{i2} ) = - p_1 p_2 $$
따라서 아래와 같이 공분산을 나타낼 수 있습니다.
$$ Cov(X_i, X_j) = -np_ip_j $$
(2) 상관관계
확률변수 상관관계를 구하는 식은 아래와 같습니다.
$$ Cor(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)} \sqrt{Var(Y)}} $$
이를 위에서 구한 공분산을 이용해 식을 표현하면,
$$ Cor(X_i,X_j) = \frac{-np_i p_j}{\sqrt{np_i(1-p_i)} \sqrt{np_j(1-p_j)}} $$
위 식을 풀면
$$ = \frac{ - \sqrt{n^2 p_i^2 p_j^2}}{\sqrt{(np_i-np_i^2)(np_j-np_j^2)}} $$
$$ = \frac{ - \sqrt{n^2p_i^2 p_j^2}}{\sqrt{n^2p_ip_j - n^2p_i^2p_j - n^2p_ip_j^2 + n^2p_i^2p_j^2}} $$
$$ - \sqrt{\frac{n^2p_ip_j(p_ip_j)}{n^2p_ip_j(1-p_i)(1-p_j}} $$
$$ - \sqrt{\frac{p_ip_j}{(1-p_i)(1-p_j)}} $$
(3) 오즈 (odd)
오즈란 성공할 확률이 실패할 확률의 몇 배인지 알려줍니다.
성공확률에서 실패할 확률을 나눈 형태입니다.
위 상관계수를 따로 분리해서 보면,
$$ \frac{p_ip_j}{(1-p_i)(1-p_j)} = \frac{p_i}{(1-p_i)} \frac{p_j}{(1-p_j)} $$
상관계수는 각 결과값의 성공확률에서 실패확률을 나눈 값들의 곱입니다.
'통계학 이야기' 카테고리의 다른 글
| 52. 정규분포(Normal Distribution) - 연속확률분포 (1) | 2023.11.14 |
|---|---|
| 51. R을 이용한 확률분포 - 다항분포 구하기 (1) | 2023.11.03 |
| 49. R을 이용한 확률분포 - 기하분포 & 음이항분포 (1) | 2023.11.01 |
| 48. 기하분포와 음이항분포 - 이산확률분포 (2) | 2023.10.31 |
| 47. R을 이용한 확률분포 - 포아송 분포 구하기 (1) | 2023.10.30 |




