생각 작업실 The atelier of thinking
49. R을 이용한 확률분포 - 기하분포 & 음이항분포 본문
Chapter 49. R을 이용한 확률분포 - 기하분포 & 음이항분포
1. R 에서의 확률분포
| 이산확률분포 | 연속확률분포 | ||
| 이항분포 | binom | 정규분포 | norm |
| 초기하분포 | hyper | T분포 | t |
| 포아송분포 | pois | F분포 | f |
| 기하분포 | geom | 카이분포 | chisq |
| 음이항분포 | nbionom | 균등분포 | unif |
| 다항분포 | multinom | 지수분포 | exp |
구하고자 하는 함수에 따라 아래의 접두사를 붙여 사용하면 됩니다.
- d : probability mass/density function - 확률 질량/밀도 함수
- p : cumulative distribution function - 누적함수
- q : quantile function - 분위수
- r : random number generator - 램덤 생성 작업
2. 기하분포(Geometric Distribution)
기하분포는 성공할 확률이 p인 베르누이 시행을 성공할 때까지 시행하는 경우 실패(시행)횟수의 분포입니다.
기하분포의 확률질량함수는 다음과 같습니다.
$$ f(x) = (1-p)^x p , x = 0.,1,2,... $$
R에서 기하분포의 확률질량함수를 구하는 함수는 "dgeom" 입니다.
dgeom(x,p)
x : 확률변수 - 실패횟수
p : 성공확률
p = 0.3 인 실패횟수가 0인 확률질량함수
x <- 0
p <- 0.3
dgeom(x,p)[1] 0.3즉, 처음 시행했을 때 성공할 확률입니다. 따라서 성공할 확률 p와 같습니다.
x가 0에서 10까지의 확률질량함수 그래프
x <-0:10
p <- 0.3
geom <- dgeom(x,p)
names(geom) <- x
barplot(geom, space = 2, col='skyblue',xlab = '실패횟수')
abline(h=0)
◈ 예제 : 동전던지기 - 앞면이 나올 때까지 던지는 실험에서 2번이내에 성공할 확률은 ?
이 경우는 누적분포함수를 구하는 'pgeom' 함수로 구할 수 있습니다.
pgeom(x,p,lower.tail=TRUE)
x : 확률변수 - 누적실패횟수
p : 성공확률
lower.tail : 누적분포확률의 방향을 나타냅니다.
TRUE : x보다 적거나 같은 값의 합
FALSE : x보다 큰 값의 합
x <- 2-1
p <- 0.5
pgeom(x,p)[1] 0.75주의해야 할 점은 매개변수 x 는 실패횟수이므로 실행횟수에서 1을 빼야합니다. 따라서 x 에는 실행횟수 2에서 1을 뺀 1로 함수를 실행해야 합니다.
누적분포함수를 그래프로 그리면,
x <- 0:9
p <- 0.5
pge <- pgeom(x,p,lower.tail = TRUE)
names(pge) <- x+1
barplot(pge, space = 2, col='skyblue',main='누적분포함수', xlab = '실행횟수',ylim =c(0,1))
abline(h=0)
abline(h=0.9,col='red')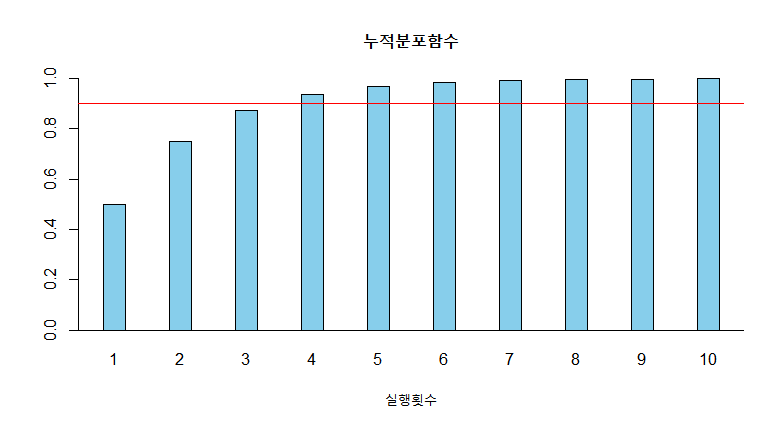
위 그래프에서 90% 이상의 성공률을 보이는 최소 실행 횟수는 4 회임을 알 수 있습니다.
3. 음이항분포(Negative Binomial Distribution)
음이항분포는 성공할 확률이 p인 베르누이 시행을 r번 성공할 때까지 시행하는 경우 실패(시행)횟수의 분포입니다.
음이항분포의 확률질량함수는 다음과 같습니다.
$$ f(x) = \binom{x+r-1}{r-1} p^r(1-p)^{x} , x=0,1,2,3,... $$
R에서 음이항분포의 확률질량함수는 'dnbinom' 입니다.
dnbinom(x,r,p)
x : 확률변수 - r번 성공할 때까지 실패한 횟수
r : 성공횟수
p : 성공할 확률
◈ 예제 : 가위바위보
5명과 차례로 가위바위보 게임을 한다고 했을 때, 비기거나 지면 계속 게임을 진행하고 이기면 다른 사람과 게임을 합니다.
(1) 가위바위보 게임을 10회만에 완료할 확률은 ?
x는 실패횟수이므로 5, r 은 5, 성공확률 p =1/3 을 차례로 함수에 적용합니다.
x <- 5 # 실패횟수
r <- 5 # 성공횟수
p <- 1/3 # 성공확률
dnbinom(x,r,p)[1] 0.06828227
(2) 가위바위보 게임을 10회 이내에 완료할 확률은 ?
이 경우는 누적확률분포함수를 구하는 'pnbinom'을 사용합니다.
pnbinom(x,r,p,lower.tail = TRUE)
x : 확률변수 - r번 성공할 때까지 실패한 횟수
r : 성공횟수
p : 성공할 확률
lower.tail : 누적분포확률의 방향을 나타냅니다.
TRUE : x보다 적거나 같은 값의 합
FALSE : x보다 큰 값의 합x <- 5 # 실패횟수
r <- 5 # 성공횟수
p <- 1/3 # 성공확률
pnbinom(x,n,p,lower.tail = TRUE)[1] 0.2131281
5회시행부터 20회 시행까지의 누적확률분포 그래프
x <- 0:20 # 실패횟수
r <- 5 # 성공횟수
p <- 1/3 # 성공확률
dnb <-pnbinom(x,r,p)
names(dnb) <- x+5
barplot(dnb, space = 2, col='skyblue',xlab = '실행횟수',ylim=c(0,1))
abline(h=0)
abline(h= 0.9, col="red")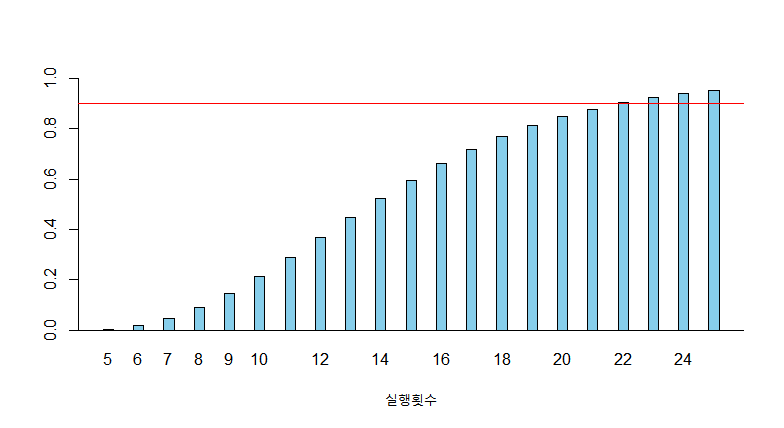
가위바위보 게임이 22회이상 실행해야 90%의 완료가능성이 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 51. R을 이용한 확률분포 - 다항분포 구하기 (1) | 2023.11.03 |
|---|---|
| 50. 다항분포(Multinomial Distribution) - 이산확률분포 (0) | 2023.11.02 |
| 48. 기하분포와 음이항분포 - 이산확률분포 (2) | 2023.10.31 |
| 47. R을 이용한 확률분포 - 포아송 분포 구하기 (1) | 2023.10.30 |
| 46. 포아송분포(Poisson Distribution) - 이산확률분포 (1) | 2023.10.27 |




