| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 산점도
- css
- JavaScript
- version 2
- 글쓰기
- 이원배치 분산분석
- 인공지능
- 가설검정
- 오블완
- 경제학
- 해운업
- 추정
- 이항분포
- 확률
- 변동분해
- 데이터 과학
- 통계학
- 정규분포
- version 1
- 반복없음
- 에세이
- r
- 혼합효과모형
- 회귀분석
- html
- 티스토리챌린지
- 고정효과모형
- 반복있음
- 변량효과모형
- 분산분석
- Today
- Total
생각 작업실 The atelier of thinking
48. 기하분포와 음이항분포 - 이산확률분포 본문
Chapter 48. 기하분포와 음이항분포
기하분포와 음이항분포는 모두 이항분포에서 파생된 분포로, 이항분포와 관련된 확률문제를 해결하는데 사용됩니다.
기하분포는 이항분포에서 성공확률이 일정하고 시행횟수가 무한히 많아지는 경우, 즉 시행횟수가 많아지면서 확률이 점점 작아지는 경우를 다루는 분포입니다. 예를 들어, 동전을 던져서 앞면이 나올 확률이 0.5로 일정하고, 앞면이 처음으로 나오는 시행횟수를 기록한다면, 이 시행횟수가 따르는 분포가 기하분포입니다. 즉 기하분포는 단일 베르누이 시행에서 첫번째 성공까지 시행한 횟수가 따르는 이산확률분포입니다.
음이항분포는 이항분포에서 시행횟수가 일정하고 성공확률이 일정한 경우(기하분포)를 다루는 대신, 시행횟수는 일정하지 않고 성공횟수가 일정한 경우를 다루는 분포입니다. 예를 들어, 동전을 던져서 앞면이 나올 확률이 0.5로 일정하고, 세번째 앞면이 나올 때까지 동전을 던지는 시행횟수를 기록한다면, 이 시행횟수가 따르는 분포가 음이항분포입니다. 즉, 음이항분포는 단일 베르누이 시행에서 성공횟수가 일정할 때 성공까지 시행한 횟수가 따르는 이산확률분포입니다.
1. 기하분포(Geometric Distribution)
(1) 기하분포의 정의 및 확률변수
기하분포는 성공할 확률이 p인 베르누이 시행을 성공할 때까지 시행하는 경우 실패 혹은 시행 횟수의 분포입니다.
표본공간은 성공을 S, 실패를 F 라 했을 때, 표본공간 Ω={S,FS,FFS,FFFS,...} 으로 표현할 수 있습니다.
확률변수는 위 표본공간에서 실패한 횟수일 경우는 0,1,2,... 가 될 것이고 시행횟수일 경우는 1,2,3,.. 으로 나타낼 수 있습니다.
기하분포는 아래와 같이 표기합니다.
X∽
(2) 기하분포의 확률질량함수
성공할 확률 p, 실패할 확률 1-p라 할 때,
f(x) = (1-p)^x p , x = 0.,1,2,...
여기서 x는 실패한 횟수를 뜻합니다.
시행한 횟수를 구하는 확률질량함수는 시행횟수를 확률변수Y 라 했을 때, 시행횟수는 실패한 횟수에 1을 더하면 됩니다. 시행횟수 Y = X+1 이라 나타낼 수 있습니다.
따라서 시행횟수 Y의 확률질량함수는 아래와 같이 표현할 수 있습니다.
f_Y(y) = (1-p)^{y-1} p , y = 1,2,3, ...
(3) 기하분포의 누적분포함수
◈ 예제 : x번째 실험(실행횟수) 이전에 성공할 확률 (누적분포함수)
우선 x번째 실험에 성공했다는 것은 x-1번 실패할 확률과 같습니다. 10번째 실험에 성공했다는 것은 9번 실패할 확률과 같다는 것입니다. 실행횟수 Y를 실패횟수 X 로 나타내면, P(Y \leq x) = P(X \leq x-1) 가 됩니다.예를 들어, 10번째 실험 이전에 성공할 확률은 1부터 10번째까지의 성공확률을 모두 더한 값이고 이는 0부터 9까지의 실패확률의 합으로 표현할 수 있습니다.
이를 일반화하여 식으로 표현하면, P(X \leq x) = \sum_{k=0}^x p(1-p)^k = p + p(1-p)+p(1-p)^2+ ... + p(1-p)^{x-1}
위 식은 첫항이 p 이고 공비가 1-p인 등비급수 형태로 나타납니다.
※ 등비급수(geometric series)의 합
등비급수란 등비수열의 부분합을 무한으로 보낸 개념입니다. 등비수열(기하수열)이란 각 항이 일정한 비를 가지는 수열을 말합니다. 등비수열의 첫항을 a, 공비를 r이라 할 때 등비수열의 n번째 항은, 아래와 같습니다. a_n = ar^{n-1} 따라서, n까지 더한 합인 등비급수를 아래와 같이 표현할 수 있습니다.
S = a + ar^1 + ar^2 + ... + ar^{n-1}
이러한 등비급수의 합은, 아래와 같이 정리할 수 있습니다.
S = a + ar^1 + ar^2 + ... + ar^x
rS = ar^1 + ar^2 + ar^3 ... + ar^{x+1}
위에서 아래를 빼면,
(1-r) S = a - ar^{x+1}
S = \frac{a-ar^{x+1}}{1-r}
이제 위 식에서 a = p , r = (1-p) 를 대입하여 정리하면,
\frac{p-p(1-p)^{x+1}}{(1-(1-p))} = \frac{p(1-(1-p)^{x+1})}{p} = 1-(1-p)^{x+1}
즉, P(X \leq x) = 1 - (1-p)^{x+1} 로 나타낼 수 있습니다.
반대로 P ( X \ge x ) 인 경우에는,
P ( X \ge x ) = 1- P(X \leq x-1) = (1-p)^x
로 나타낼 수 있습니다.
(4) 무기억성(memoryless)
무기억성이란 처음 시작할 때 확률이 x번 실패했다 하더라도 지금 다음 시행에서 성공할 확률은 이 앞에 실패한 것은 기억하지 않고 그냥 처음 시행 때와 똑같다라는 것입니다.
즉, 동전던지기에서 5번 연속 뒷면이 나왔다고 하더라고 6번째가 앞면이 나올 확률은 0.5 라는 것입니다.
팡쪽에서 뒷면이 많이 나왔다고 해서 새로운 시행 앞면이 나올 확률이 0.5 보다 높은 0.7,0.8 이 될 수는 없습니다.
현실에서 야구 중계를 보다보면 3할타자가 1,2타석에서 안타를 못치고 세번째 타석에 들어서면 "이제 안타를 치겠군요." 라고 거의 100% 칠 것처럼 하는 멘트를 많이 듣지만, 이것은 희망사항일 뿐, 통계적인 확률은 0.3 에 불과하다는 것입니다.
x번째까지 실패했다고 할 때, 다음 x+1번째 시행에서의 성공확률을 식으로 표현하면, 아래와 같습니다.
x번째 실패했다는 것은 x+1번째 이후 성공했다는 것이라 할 수 있습니다.즉, P ( X \ge x) = 1- P(X \leq x-1) = (1-p)^x 로 나타낼 수 있습니다.또한, "~할 때" 라는 것은 조건부 확률이라는 것을 의미합니다. 따라서 위 문제를 식으로 표현하면, P(X=x | X \ge x) 구하라는 것입니다. 이 식을 풀면,
P(X=x | X \ge x) = \frac{P(X=x, X \ge x)}{P(X \ge x)}= \frac{f_X(x)}{P(X \ge x)}
= \frac{(1-p)^x p}{(1-p)^x} = p
x+1번째 시행에서의 성공확률은 처음 확률 p 란 결과가 나옵니다. 무기억성을 표현한 것입니다.
(5) 기대값
확률변수 X를 실패횟수라 했을 때 기대값은 아래와 같이 나타낼 수 있습니다.
E(X) = \sum_{x=0}^{\infty} xf(x) = \sum_{x=0}^{\infty}xp(1-p)^x
= p(1-p) + 2p(1-p)^2+ 3p(1-p)^3 + ...
이 식은 첫항이 p(1-p), 공비는 1-p 인 무한 등비급수입니다.
※ 무한등비급수의 합
S = ar + 2ar^2 + 3ar^3 +4ar^4+ ...
rS = ar^2 + 2ar^3 + 3ar^4 ...
위에서 아래를 빼면,
(1-r) S = ar^1 + ar^2+ar^3+... = \frac{ar}{1-r}
S = \frac{ar}{(1-r)^2}
이 식을 기대값 식에 적용하면
E(X) = \frac{p(1-p)}{(1-(1-p)}^2 = \frac{p(1-p)}{p^2} = \frac{1-p}{p}
즉, 기대값은 실패할 확률에서 성공할 확률을 나눈 값입니다.
확률변수 Y를 실행횟수라 했을 때 기대값은 아래와 같이 나타낼 수 있습니다.
Y = X+1 이므로 기대값은,
E(Y) = E(X+1) = \frac{1}{p}
로 나타낼 수 있습니다.
◈ 예제 : 동전던지기 - 앞면이 나올 때까지 던지는 실험 ( 앞면 : 성공, 뒷면 : 실패 )
(1) 2번이내에 성공할 확률은 ?
실행횟수 2번이내에 실패횟수 1번의 확률을 구하는 것이라 할 수 있습니다.
따라서 성공확률 p = \frac{1}{2} , 실패횟수 : X, 실행횟수 : Y , Y=X+1 라면,
P(Y \leq 2) = \frac{1}{2} + (\frac{1}{2})^2 = 0.75
2번이내에 성공할 확률은 0.75 입니다.
(2) 90%이상 성공률을 보이는 최소 실행횟수는 ?
문제를 식으로 표현하면 P(Y \leq y) \ge 0.9 를 만족하는 y를 구하라는 것입니다.
P(Y \leq y) = 1 - (1-p)^y
에서 p=\frac{1}{2} 을 대입하여 계산해보면,
P(Y \leq y) = 1 -(\frac{1}{2})^2 \ge 0.9
(\frac{1}{2})^y \leq 0.1 → y \ge 4
4회이상 실행하면 90%이상 앞면이 나오는 것을 알 수 있습니다.
(3) 앞면이 나올 실행횟수 기대값은 ?
E(Y) = \frac{1}{p} = \frac{1}{\frac{1}{2}} = 2
평균 2회 실행하면 앞면이 나올 것으로 기대합니다.
기하분포는 성공횟수가 아닌 성공을 위한 실행횟수에 관심을 가질 때 주로 사용합니다.
2. 음이항분포 (Negative Binomial Distribution)
(1) 음이항분포의 정의 및 확률변수
음이항분포는 성공할 확률이 p인 베르누이 시행을 r번 성공할 때까지 시행하는 경우 실패(시행)횟수의 분포입니다.
표본공간은 성공을 S, 실패를 F 라 했을 때, S를 3번 성공할 때까지라 한다면, S가 3번, 표본공간 \Omega = \{ SSS,FSSS,SSFS,SFSS, ... \} 으로 표현할 수 있습니다.
확률변수는 위 표본공간에서 실패한 횟수일 경우는 0,1,2,... 가 될 것이고 시행횟수일 경우는 r,r+1,r+2,r+3,.. 으로 나타낼 수 있습니다.
음이항분포는 아래와 같이 표기합니다.
Y \backsim NB(r,p)
(2) 음이항분포의 확률질량함수
실패횟수를 X , 성공횟수를 r, 시행횟수를 Y라 하면, Y=X+r 입니다.
Y = y 라 하면 y번째는 성공(S) 입니다. (시행횟수 기준)y-1번째까지의 결과는 r-1번의 성공(S)과 y-r개의 실패(F)로 이루어져 있습니다.
y-1번째까지의 결과를 일반화하면,
f_Y(y) = \binom{y-1}{r-1} p^{r-1}(1-p)^{y-r} , y = r,r+1,r+2. ...
y-1번째까지는 이항분포를 형성하는 것을 알 수 있습니다.
위 식에 y의 성공확률 p를 곱하면 y 번째의 확률을 구할 수 있습니다.
따라서 실행횟수 Y의 확률질량함수는 아래와 같습니다.
f_Y(y) = \binom{y-1}{r-1} p^r(1-p)^{y-r}
X=x 라 하면, x+r번째는 성공(S)입니다. (실패횟수 기준)x+r-1번째까지의 결과는 r-1개의 성공(S)과 x개의 실패(F)로 이루어져 있습니다.따라서 실패횟수 X의 확률질량함수는 아래와 같습니다.
f(x) = \binom{x+r-1}{r-1} p^r(1-p)^{x} , x=0,1,2,3,...
(3) 음이항분포의 기대값
실패횟수 X , 성공횟수 r, 시행횟수 Y라 할 때, 기대값은 각각의 합이라 할 수 있습니다.
베르누이 시행이므로 각각은 독립입니다.
실패횟수의 기대값은,
X = X_1+X_2+...+X_r
E(X) = E(X_1+X_2+...+X_r) = r \frac{(1-p)}{p}
시행횟수의 기대값은,
Y = Y_1+Y_2+...+Y_r
E(Y) = E(Y_1+Y_2+...+Y_r) = r \frac{1}{p}
◈ 예제 : 가위바위보
5명과 차례로 가위바위보 게임을 한다고 했을 때, 비기거나 지면 계속 게임을 진행하고 이기면 다른 사람과 게임을 합니다.
(1) 가위바위보 게임을 10회만에 완료할 확률은 ?
이 경우를 식으로 표현하면, p = \frac{1}{3} 이고 r=5 일 때 P(Y=10) 을 구하라는 것입니다.
f_Y(y) = \binom{y-1}{r-1} p^r(1-p)^{y-r}
f_Y(10) = \binom{10-1}{5-1}(\frac{1}{3})^5(\frac{2}{3})^{10-5} = 0.068
(2) 가위바위보 게임을 10회 이내에 완료할 확률은 ?
이 경우는 누적확률분포를 사용해야 합니다. 이를 식으로 나타내면, 아래와 같습니다.
f_Y(10) = \sum_{y=5}^{10} \binom{y-1}{5-1}(\frac{1}{3})^y(\frac{2}{3})^{y-5} = 0.213
(3) 5회 승리하기 위하여 게임 시행횟수에 대한 기대값은 ?
E(Y) = r \frac{1}{p} = 5 \frac{1}{\frac{1}{3}} = 15
시행횟수의 기대값은 15회입니다.
3. 기하분포 vs 음이항분포
| 기하분포 | 음이항분포 | |
| 확률질량함수 f(x) | (1-p)^x p , x = 0.,1,2,... | \binom{x+r-1}{r-1} p^r(1-p)^{x} , x=0,1,2,3,... |
| 확률질량함수 f_Y(y) | (1-p)^{y-1} p , y = 1,2,3, ... | \binom{y-1}{r-1} p^r(1-p)^{y-r} |
| 확률분포 표시 | X \backsim Geo(p) | Y \backsim NB(r,p) |
| 기대값 E(X) | \frac{1-p}{p} | r \frac{(1-p)}{p} |
| 기대값 E(Y) | \frac{1}{p} | r \frac{1}{p} |
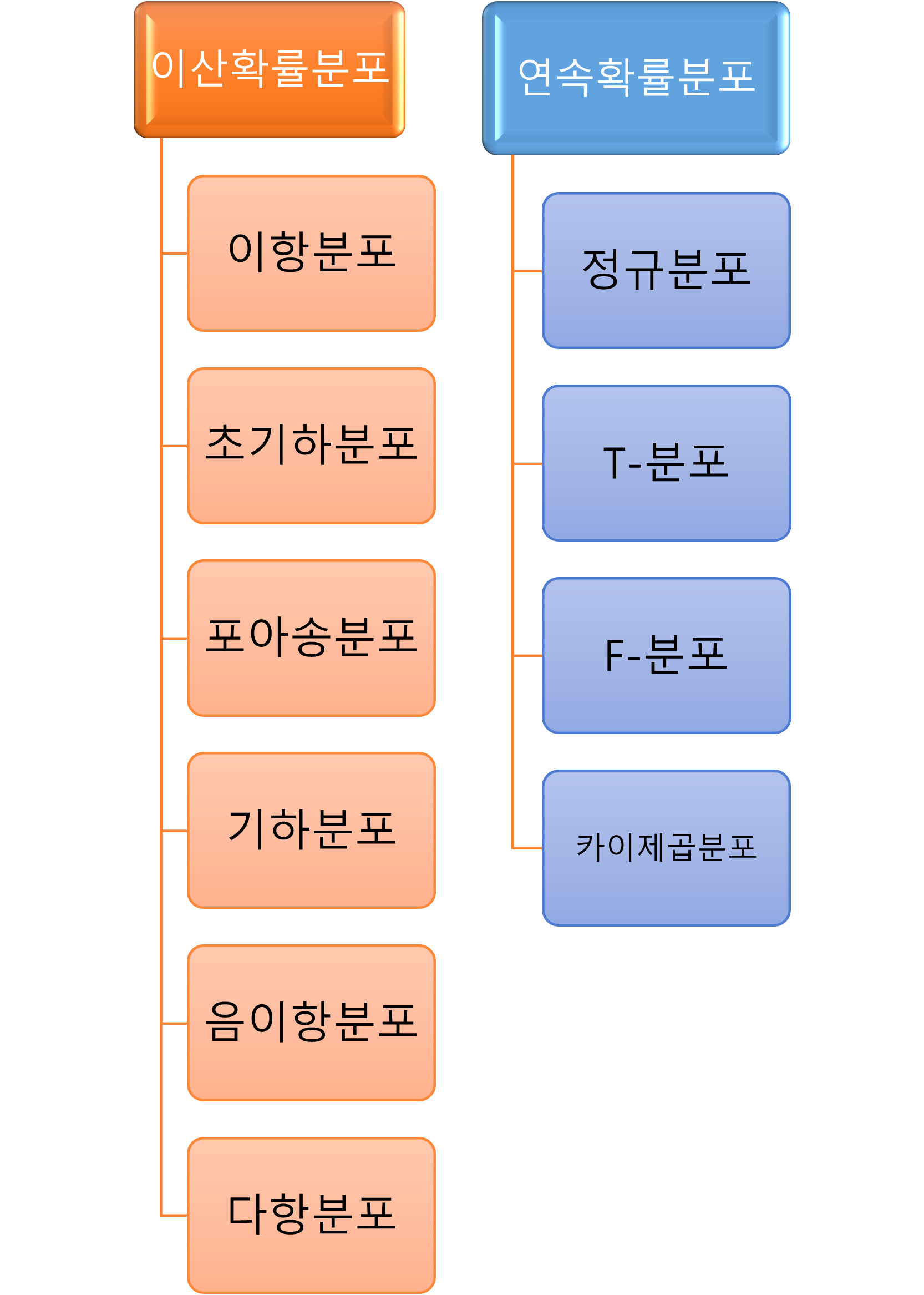
확률분포의 분류
'통계학 이야기' 카테고리의 다른 글
| 50. 다항분포(Multinomial Distribution) - 이산확률분포 (0) | 2023.11.02 |
|---|---|
| 49. R을 이용한 확률분포 - 기하분포 & 음이항분포 (1) | 2023.11.01 |
| 47. R을 이용한 확률분포 - 포아송 분포 구하기 (1) | 2023.10.30 |
| 46. 포아송분포(Poisson Distribution) - 이산확률분포 (1) | 2023.10.27 |
| 45. R을 이용한 확률분포 - 초기하분포 구하기 (1) | 2023.10.26 |




