| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- JavaScript
- 혼합효과모형
- 이항분포
- 고정효과모형
- 티스토리챌린지
- 분산분석
- 반복없음
- 글쓰기
- 변량효과모형
- 에세이
- 산점도
- 통계학
- css
- 추정
- 반복있음
- 오블완
- 이원배치 분산분석
- 정규분포
- 가설검정
- 인공지능
- 데이터 과학
- 회귀분석
- html
- version 2
- 경제학
- 확률
- 해운업
- r
- 변동분해
- version 1
- Today
- Total
생각 작업실 The atelier of thinking
71. 모비율에 대한 통계적 추론 II 본문
Chapter 71. 모비율에 대한 통계적 추론 II
정확한 모수 추정을 위해서는 전수 조사를 한다면 가장 정확하겠지만, 현실적으로 어려움이 많기 때문에 표본조사를 하게 됩니다. 하지만, 표본 수집이라 해도 많은 비용이 들기도 하고, 시간 등의 제약조건이 있습니다.
그렇다고 표본이 너무 적다면 신뢰도에 문제가 생길 수 있습니다. 즉, 표본크기는 모수 추정의 정확도 및 신뢰도에 영향을 줍니다. 따라서 모수 추정을 위한 표본크기는 정확도와 신뢰도, 비용과 시간을 고려한 최적의 크기를 정해야 합니다.
여기서 신뢰도는 신뢰수준을 통하여 , 정확도는 오차범위로 나타낼 수 있습니다.
통계학 추론의 두 방법인 구간추정과 가설검정에 기반한 표본크기 결정방법에 대하여 알아보겠습니다.
1. 구간 추정에 기반한 표본크기 결정방법
모평균과 마찬가지로 신뢰구간은 아래와 같이 나타낼 수 있습니다.

다만 모평균 (μ) 대신에 모비율 (θ) 을 사용하여 구할 수 있습니다. 모비율 (θ) 를 기준으로 수식으로 표현하면 아래와 같습니다.
100(1−α) 신뢰수준에서 허용오차범위가 ±δ
P(|P−θ|<δ)=1−α
정규근사이므로 정규분포 분위수를 사용합니다. n을 기준으로 정리하면 아래와 같습니다.
δ=zα/2√θ(1−θ)n
⟹n=(zα/2δ)2θ(1−θ)
θ 에 대한 정보가 없는 경우 모든 θ 에 대해 성립하도록 n을 결정하기 위해서, θ(1−θ) 는 θ 가 0.5일 때 가장 큽니다.
n=(zα/2δ)214
◈ 예제 : 여론 조사
95% 신뢰수준에서 오차범위가 5%(0.05)이내의 결과를 내기 위한 여론 조사를 최소 몇 명을 조사해야 하는가?
n=(zα/2δ)214
θ 가 0.5일 때를 계산해보면
(1.960.05)214=384.16
θ 에 0.5를 대입하여 계산하면 384.16 으로 최소 385명을 조사해야 합니다.
2. 가설검정을 위한 표본크기 결정
(1) 가설 설정
모평균과 마찬가지로 유효효과 δ 로 가설 설정을 할 수 있습니다.
귀무가설 H0:θ=θ0vs 대립가설 H1:θ=θ1=θ0+δ
(2) 검정 통계량
Z0=P−θ0√θ0(1−θ0)/n≃N(0,1)
모비율을 표준화하면 표준정규분포에 근사합니다.
(3) 유의수준
P(P−θ√θ0(1−θ)/n>Zα|H0)≈α
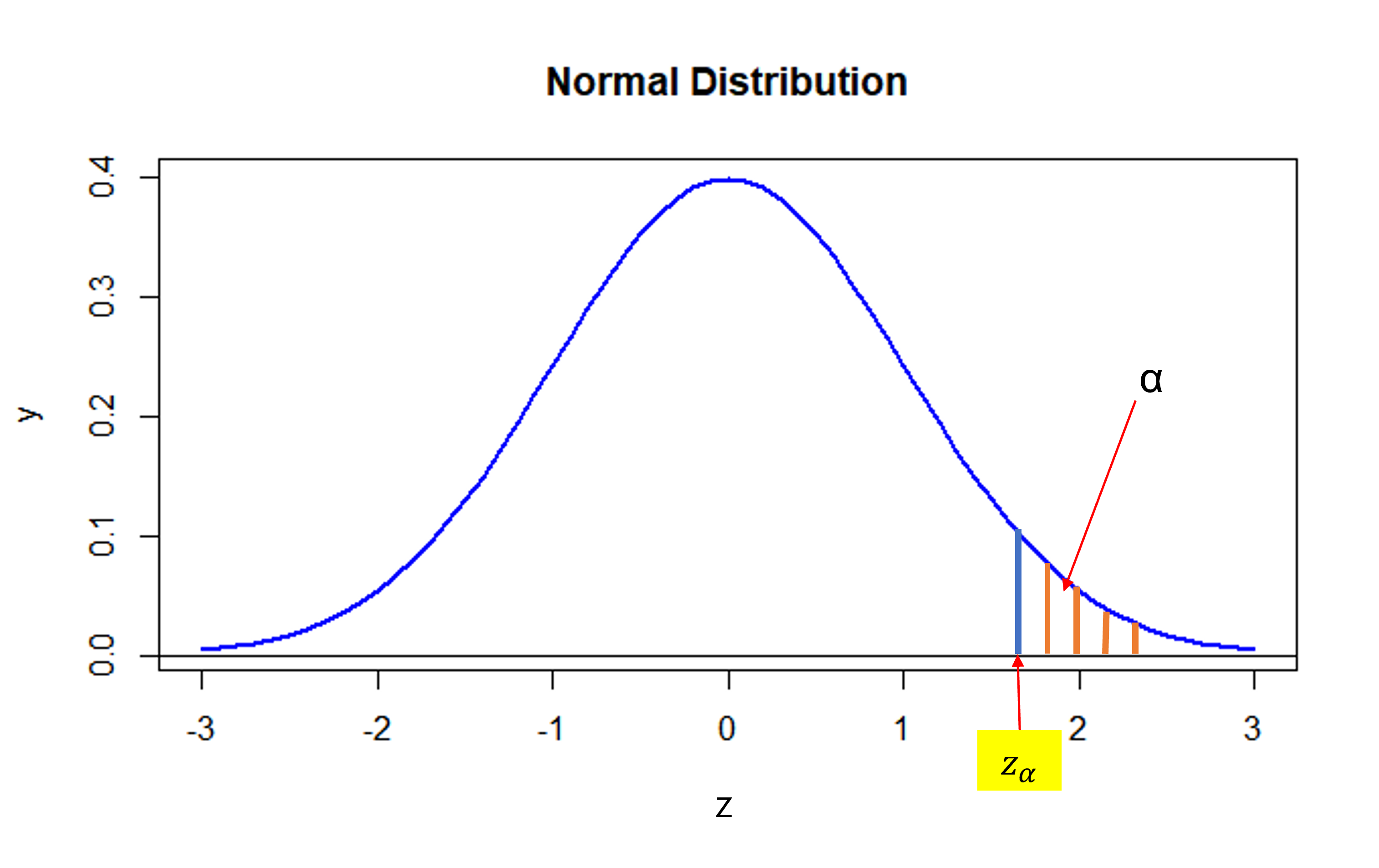
(4) 검정력
P(P−θ√θ0(1−θ)/n>Zα|H1)
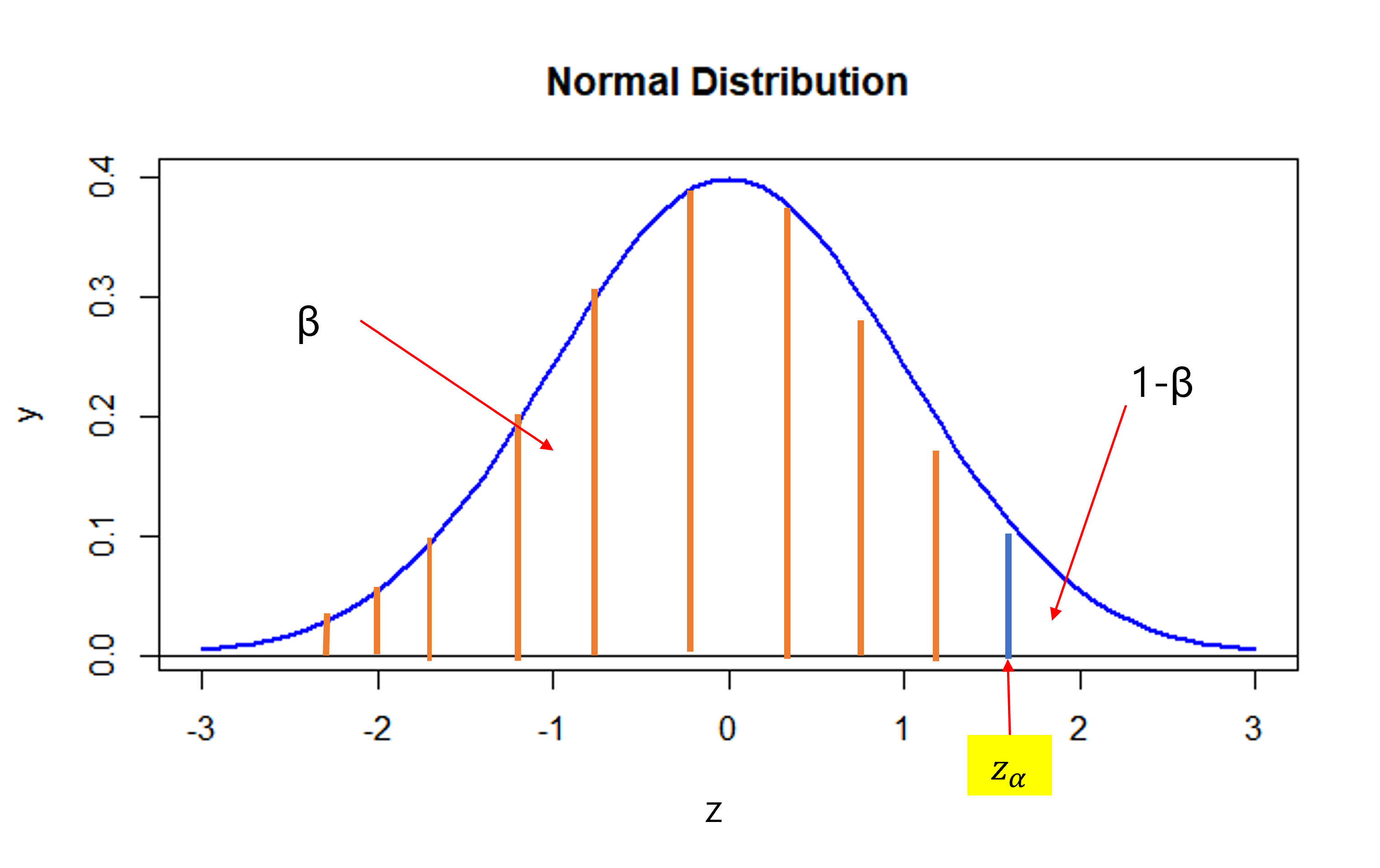
1−β=P(P>θ0+Zα√θ0(1−θ0)/n|H1)
H1:P−θ1√θ1(1−θ1)/n≃N(0,1)
⟹1−β=1−Φ(θ0−θ1+Zα√θ0(1−θ0)/nθ1(1−θ1)/n)
⟹−δ+zα√θ0(1−θ0)/n=−zβ√θ0(1−θ0)/n
⟹√nδ=zα√θ0(1−θ0)/n+zβ√θ1(1−θ1)/n
(5) 가설검정을 의한 표본크기
위 식을 표본크기 n으로 정리하면,
n=(zα√θ0(1−θ0)+zβ√θ1(1−θ1))2δ2
'통계학 이야기' 카테고리의 다른 글
| 73. 두 모집단의 비교 - 독립표본 & 대응표본 (0) | 2024.06.14 |
|---|---|
| 72. R 을 이용한 모비율에 대한 통계적 추론 (1) | 2024.06.13 |
| 70. 모비율에 대한 통계적 추론 I (1) | 2024.06.11 |
| 69. R을 이용한 카이제곱분포 및 모분산 추정 (2) | 2024.06.10 |
| 68. 모분산에 대한 통계적 추론 (1) | 2024.06.09 |




