생각 작업실 The atelier of thinking
77. R을 이용한 두 그룹의 평균 비교 본문
Chapter 77. R을 이용한 두 그룹의 평균 비교
두 그룹의 평균을 비교할 때 사용할 수 있는 R의 함수는 t.test( )입니다.
앞서 단일 모집단의 모평균을 추론할 때에도 t.test( )를 사용했었습니다.
▶ t.test( )
t.test(x, y = NULL,
alternative = c("two.sided", "less", "greater"),
mu = 0, paired = FALSE,
conf.level = 0.95, var.equal = FALSE ...)
x : 일표본 또는 이표본 데이터 셋이거나 차이가 평가되는 대응표본 데이터 셋
y : 비교할 이표본 데이터 셋. 일표본 또는 대응표본 t-검정의 경우에는 NULL로 설정
alternative: 검정의 양측성(two.sided) 또는 단측성(less, greater)을 설정,
기본값은 "two.sided"
mu: 일표본 또는 이표본 t-검정의 경우에 대한 귀무가설의 평균 값. 기본값은 0.
paired: 대응표본 t-검정을 수행할 때 TRUE로 설정. 기본값은 FALSE
conf.level: 신뢰구간을 설정, 기본값은 0.95
var.equal : 푸 표본의 분산이 동일한 지 여부, 기본값은 FALSE
◆ 예제 : 신체검사 자료
1. 자료 불러오기
health <- read.csv("신체검사.csv",header = TRUE, fileEncoding = "CP949",
encoding = "UTF-8")
head(health)
ID 나이 성별 수축혈압 이완혈압 콜레스테롤1 콜레스테롤2
1 1 42 F 120 95 196 220
2 2 53 M 122 72 230 232
3 3 53 M 132 88 242 223
4 4 48 F 128 79 239 209
5 5 53 F 118 74 204 198
6 6 58 F 130 72 210 245
성인 50명의 신체검사 자료 입니다.
혈압과 운동전후의 콜레스테롤 수치를 나타내는 자료입니다.
위 자료는 데이터프레임, 즉 표 형태의 자료입니다.
▶ dim( ) 함수는 데이터프레임의 형태를 알아볼 수 있는 함수입니다.
dim(health)[1] 50 7
50 은 표본 수를 나타내고 7은 변수의 수를 나타냅니다.
위 표에서 row,column 으로 자료의 크기를 보여주고 있습니다.
2. 독립표본인 경우
◆ 예제 : 신체검사 자료
남녀별로 수축혈압과 이완혈합의 평균에 차이가 있는지 각각 5% 유의수준에서 검정한다면?
(1) 분산이 같다고 가정했을 때
"var.equal = TRUE" 은 분산이 같다는 설정입니다. 기본값은 "FALSE"로 분산이 서로 다른 것으로 설정합니다.
"t.test(타겟변수~범주형변수, data= )"으로 사용할 수 있습니다.
t.test(수축혈압~성별, data = health, var.eq=T)
Two Sample t-test
data: 수축혈압 by 성별
t = -2.6916, df = 48, p-value = 0.009759
alternative hypothesis: true difference in means between group F and
group M is not equal to 0
95 percent confidence interval:
-29.063773 -4.208954
sample estimates:
mean in group F mean in group M
134.8636 151.5000
대립가설은 "남녀의 수축혈압은 차이가 있다" 로 설정되었습니다.
p-value는 0.009759 이므로 5% 유의수준에서 귀무가설은 기각되고, 대립가설을 채택합니다. 즉 "남녀별로 수축혈압은 유의미한 차이가 있다"라고 할 수 있습니다.
이를 시각화하면,
boxplot(수축혈압~성별,health, col=c("pink","skyblue"),boxwex=0.5)
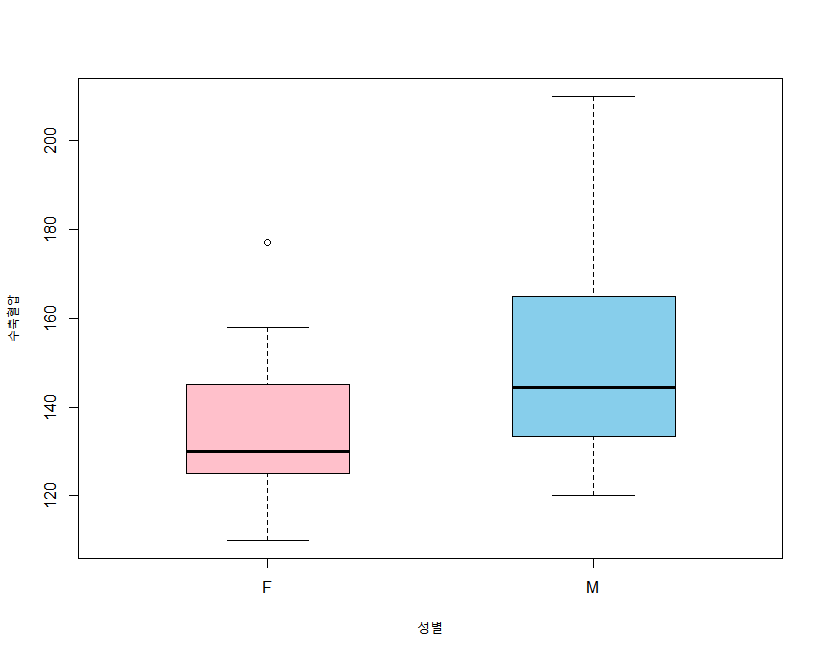
남녀별 이완혈압을 분산이 같다고 가정하여 검정하면,
t.test(이완혈압~성별, data = health, var.eq=T)
Two Sample t-test
data: 이완혈압 by 성별
t = -1.5252, df = 48, p-value = 0.1338
alternative hypothesis: true difference in means between group F and
group M is not equal to 0
95 percent confidence interval:
-8.994456 1.234716
sample estimates:
mean in group F mean in group M
85.22727 89.10714
p-value는 0.1338 이므로 5% 유의수준에서 귀무가설은 유지됩니다. 즉 "남녀별로 이완혈압은 유의미한 차이가 없다"라고 할 수 있습니다.
이를 시각화하면,
boxplot(이완혈압~성별,health, col=c("pink","skyblue"),boxwex=0.5)

(2) 분산이 다르다고 가정할 때
var.equal의 기본값은 FALSE이므로 생략하면 분산이 다르다는 가정으로 검정합니다.
t.test(수축혈압~성별, data = health) Welch Two Sample t-test
data: 수축혈압 by 성별
t = -2.828, df = 46.581, p-value = 0.006884
alternative hypothesis: true difference in means between group F and
group M is not equal to 0
95 percent confidence interval:
-28.473572 -4.799155
sample estimates:
mean in group F mean in group M
134.8636 151.5000
p-value는 0.006884 이므로 5% 유의수준에서 귀무가설은 기각되고, 대립가설을 채택합니다. 즉 "남녀별로 수축혈압은 유의미한 차이가 있다"라고 할 수 있습니다. 앞서 분산이 같을 때보다 p-value가 더 낮게 나타납니다.
이완혈압의 경우는 아래와 같습니다.
t.test(이완혈압~성별, data = health)
Welch Two Sample t-test
data: 이완혈압 by 성별
t = -1.5199, df = 44.623, p-value = 0.1356
alternative hypothesis: true difference in means between group F and
group M is not equal to 0
95 percent confidence interval:
-9.022359 1.262619
sample estimates:
mean in group F mean in group M
85.22727 89.10714
p-value는 0.1356 이므로 5% 유의수준에서 귀무가설은 유지됩니다. 즉 "남녀별로 이완혈압은 유의미한 차이가 없다"라고 할 수 있습니다.
3. 대응표본인 경우
◆ 예제 : 신체검사 자료
콜레스테롤1은 운동 전, 콜레스테롤2는 운동 후의 콜레스테롤 양이라고 하면, 운동에 의해 콜레스테롤이 줄었는지 5% 유의수준에서 검정한다면?
"paried = TRUE"는 짝비교를 설정합니다.
t.test(health$콜레스테롤1,health$콜레스테롤2,paired = T) Paired t-test
data: health$콜레스테롤1 and health$콜레스테롤2
t = 2.7237, df = 49, p-value = 0.00892
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
3.445288 22.834712
sample estimates:
mean difference
13.14
위에서 줄었다는 의미는 1에서 2를 뺀 값이 0보다 크다는 것을 의미합니다. 따라서 alternative="great" 를 추가하여 검정합니다.
t.test(health$콜레스테롤1,health$콜레스테롤2,paired = T, alternative = "great") Paired t-test
data: health$콜레스테롤1 and health$콜레스테롤2
t = 2.7237, df = 49, p-value = 0.00446
alternative hypothesis: true mean difference is greater than 0
95 percent confidence interval:
5.051884 Inf
sample estimates:
mean difference
13.14
p-value는 0.00446 이므로 5% 유의수준에서 귀무가설은 기각되고, 대립가설을 채택합니다. 즉,"운동에 의해 콜레스테롤은 의미있는 차이로 줄었다"라고 할 수 있습니다.
위 대응표본의 짝비교를 단일 모평균 추론으로 검정할 수 있습니다.
diff <- health$수축혈압 - health$이완혈압
t.test(diff)
One Sample t-test
data: diff1
t = 2.7237, df = 49, p-value = 0.00446
alternative hypothesis: true mean is greater than 0
95 percent confidence interval:
5.051884 Inf
sample estimates:
mean of x
13.14
p-value는 0.00446 이므로 5% 유의수준에서 귀무가설은 기각되고, 대립가설을 채택합니다. 위 대응표본의 짝비교와 같은 결과가 나옵니다.
'통계학 이야기' 카테고리의 다른 글
| 79. R 을 이용한 F분포 및 등분산성 검정 (0) | 2024.06.21 |
|---|---|
| 78. 두 그룹간 분산 비교 - F 분포 (2) | 2024.06.20 |
| 76. 두 그룹간 평균 비교 - 대응표본 (1) | 2024.06.18 |
| 75. 두 그룹간 평균 비교 - 독립표본 II (2) | 2024.06.17 |
| 74. 두 그룹간 평균 비교 - 독립표본 I (0) | 2024.06.16 |




