| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- html
- 변동분해
- 티스토리챌린지
- 추정
- 오블완
- 글쓰기
- 반복있음
- 이항분포
- 경제학
- 변량효과모형
- 데이터 과학
- version 2
- 정규분포
- 인공지능
- 이원배치 분산분석
- r
- 반복없음
- 가설검정
- 에세이
- 해운업
- 확률
- css
- 고정효과모형
- JavaScript
- 산점도
- 통계학
- 회귀분석
- 분산분석
- version 1
- 혼합효과모형
- Today
- Total
생각 작업실 The atelier of thinking
21. R을 이용한 표준화 - 표준점수 구하기 본문
Chapter 21. R을 이용한 표준화 - 표준점수 구하기
지난 회차에서 정규분포를 표준 정규 분포로 만들기 위해 필요한 표준화에 대해 알아봤습니다.
2023.09.13 - [통계학 이야기] - 20. 수치자료의 형태 - 정규분포
20. 수치자료의 형태 - 정규분포
Chapter 20. 수치자료의 형태 - 정규분포 1. 분포의 형태 분포란 자료가 어떤 값들을 가지고 나타나는지를 보여주는 방법입니다. 자료 분포의 형태를 보면 보다 많은 정보를 얻을 수 있습니다. 따라
thinking-atelier.tistory.com
주변에서 접하게되는 표준화의 예제가 수능 표준 점수가 아닌가 싶습니다. 아래 예제를 통해 R을 이용하여 표준점수와 등급을 구해보겠습니다.
◈ 예제 : 수능 표준 점수와 등급 구하기
학생 A와 B가 수능에서 각각 한국지리와 세계사를 선택하였을 경우 성적을 공정하게 비교할 수 있을까?
두 과목 점수의 모집단분포가 정규분포를 따른다고 가정할 수 있지만 평균과 분산은 다르다.
A는 한국지리에서 46점, B는 세계사에서 48점을 받았다고 가정하자.
한국지리를 택한 전체 수험생 점수의 평균은 40점, 표준편차는 4점이고, 세계사의 경우 평균이 42점, 표준편차가 3점이라고 하자.
1. 두 명의 표준점수는 ?
이 경우 원 점수를 다음과 같은 절차를 거쳐서 평균이 50과 분산이 10인 표준점수로 환산하여 비교할 수 있습니다.
(1) 원 점수를 표준화를 합니다.

위 식에 각 학생의 점수와 과목 평균 및 표준편차를 대입하여 계산합니다.
▶ 학생 A : 한국지리 46 , 한국지리 평균 40, 표준편차 4
(46-40)/41.5
▶ 학생 B : 세계사 48, 세계사 평균 42, 표준편차 3
(48-42)/32
이렇게 구한 표준화된 점수는 둘 다 평균이 0 이고 표준편차가 1인 표준정규분포를 따릅니다.
(2) 표준화된 점수를 표준점수로 변환
표준화된 점수를 평균이 50점이며 표준편차가 10인 표준점수로 변환합니다.
이렇게 하기 위해 표준화된 점수에 표준점수의 편차 10을 곱하고 평균 50을 더해줍니다.
▶ 학생 A : 한국지리 표준점수 65
A <-(46-40)/4
A*10+5065
▶ 학생 B : 세계사 표준점수 70
B<-(48-42)/3
B*10+5070
2. 등급 구하기
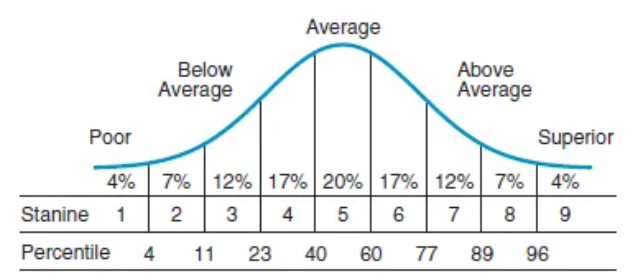
수능 등급은 9 등급으로 위 그림을 표로 정리하면,
| 등급 | 비율(%) |
| 1 | 0 ~ 4 |
| 2 | 4 ~ 11 |
| 3 | 11 ~ 23 |
| 4 | 23 ~ 40 |
| 5 | 40 ~ 60 |
| 6 | 60 ~ 77 |
| 7 | 77 ~ 89 |
| 8 | 89 ~ 96 |
| 9 | 96 ~ 100 |
등급을 알기위해서는 표준화된 점수의 백분율 알아야 합니다.
▶ pnorm( ) 함수
정규분포의 누적 확률 분포를 구하는 함수입니다.
pnorm(q, mean = 0, sd = 1, lower.tail =TRUE)
q : 확률변수가 어떤 값보다 작거나 같은 확률을 계산
mean : 정규분포의 평균값, 기본값은 0
sd : 정규분포의 표준편차, 기본값은 1
lower.tail : TRUE인 경우 누적분포함수의 하한값을 계산, 기본값
FALSE인 경우, 누적분포함수의 상한값을 계산
▶ 학생 A : 표준화된 Z 값은 1.5, 하위로부터 누적은 93% 이고, 상위로 부터 누적은 6.6% 따라서 2등급입니다.
pnorm(A) # A = 1.5
pnorm(A,lower.tail = FALSE)
▶ 학생 B : 표준화된 Z 값은 2, 하위로부터 누적은 97.7% 이고, 상위로 부터 누적은 0.02% 따라서 1등급입니다.
pnorm(B) # B = 2
pnorm(B,lower.tail = FALSE)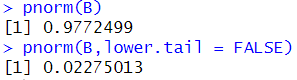
3. 등급컷을 구하려면 ?
한국지리, 세계사에서 1 등급을 받기 위해서 점수는 얼마여야 하나?
방법은 먼저 96백분위수를 찾고 원점수 기준으로 표준편차를 곱하고 평균을 더하면 됩니다.
▶ qnorm( ) 함수
표준정규 분포에서 분위수를 구해주는 함수입니다.
qnorm(p, mean = 0, sd = 1, lower.tail =TRUE)
p : 분위수를 계산하고자 하는 확률값
mean : 정규분포의 평균값, 기본값은 0
sd : 정규분포의 표준편차, 기본값은 1
lower.tail : TRUE인 경우 왼쪽 꼬리를 기준으로 계산, 기본값
FALSE인 경우, 오른쪽 꼬리를 기준으로 계산▶ 학생 A : 한국지리에서 1등급 컷은 47점입니다.
round(qnorm(0.96)*4+40)47
▶ 학생 B : 세계사에서 1등급 컷은 47점입니다.
round(qnorm(0.96)*3+42)47
참고로 각 등급컷 분위수는 아래와 같습니다.
qnorm(0.96)
qnorm(0.89)
qnorm(0.77)
qnorm(0.6)
qnorm(0.4)
qnorm(0.23)
qnorm(0.11)
qnorm(0.04)
4. 함수로 표준점수와 등급 구하기
원점수,과목평균,표준편차를 넣으면 표준점수와 등급이 나오게 끔 함수로 작성해 보았습니다.
grade <- function(t,m,s){
g <-(t-m)/s
s1 <- g*10+50
g2 <-pnorm(g)
is_grade<- ifelse (g2>=0.96,"1등급",
ifelse(pnorm(g)>=0.89,"2등급",
ifelse(pnorm(g)>=0.77,"3등급",
ifelse(pnorm(g)>=0.60,"4등급",
ifelse(pnorm(g)>=0.40,"5등급",
ifelse(pnorm(g)>=0.23,"6등급",
ifelse(pnorm(g)>=0.11,"7등급",
ifelse(pnorm(g)>=0.04,"8등급",
ifelse(pnorm(g)>=0,"9등급",
)))))))))
result <-c(s1,is_grade)
return(result)
}▶ 학생 A 의 원점수, 한국지리 평균, 표준편차를 순서대로 입력하였습니다.
grade(46,40,4)
65점, 2등급을 알 수 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 23. R을 이용하여 왜도, 첨도 구하기 (0) | 2023.09.19 |
|---|---|
| 22. 수치자료의 형태 - 왜도, 첨도 (0) | 2023.09.18 |
| 20. 수치자료의 형태 - 정규분포 (0) | 2023.09.13 |
| 19. R을 이용한 수치자료의 산포 구하기 (0) | 2023.09.11 |
| 18. 수치자료의 산포 - 분산, 표준편차,분위수 (0) | 2023.09.11 |




