생각 작업실 The atelier of thinking
19. R을 이용한 수치자료의 산포 구하기 본문
Chapter 19. R을 이용한 수치자료의 산포 구하기
R을 이용하여 범위,IQR,분산,표준편차 등 수치자료의 산포(퍼짐)를 구해보겠습니다.
지난 18회차에 수치자료의 산포에 대해 알아봤습니다.
2023.09.11 - [통계학 이야기] - 18. 수치자료의 산포 - 분산, 표준편차,분위수
18. 수치자료의 산포 - 분산, 표준편차,분위수
Chapter 18. 수치자료의 산포 1. 산포 (dispersion, 퍼짐) 산포란 자료들이 얼마나 퍼져 있는지를 나타내는 측도입니다. 중심위치와 더불어 일변량 수치형 자료요약의 한 축을 담당합니다. 데이터의 중
thinking-atelier.tistory.com
1. 자료 불러오기
◈ 예제 : 어느 고등학교 수학 중간고사 점수 (27명)
[ 98,75,46,80,76,65,90,85,75,54,68,78,84,96,44,78,78,68,92,85,77,56,70,80,84,72,73 ]
m_score <- scan()
98 75 46 80 76 65 90 85 75 54 68 78 84 96
44 78 78 68 92 85 77 56 70 80 84 72 73
2. 범위(Range)
범위는 자료 중 가장 큰 값(최대값)과 가장 작은 값(최소값)의 차이입니다.
▶ range( ) 함수
주어진 데이터의 최대값과 최소값을 반환하는 함수입니다.
range(m_score)
▶ diff( ) 함수
데이터의 차이를 나타내는 함수입니다.
range( ) 함수는 단지 최대값과 최소값을 반환할 뿐이라 차이를 구하는 diff() 함수를 사용합니다.
diff(range(m_score))
▶ max( ), min( )
최대값, 최소값을 반환해주는 함수입니다.
직접적으로 최대값에서 최소값을 빼면 범위를 구할 수 있습니다.
max(m_score)-min(m_score)
3. 사분위(간) 범위 ( Interquartile-Range)
사분위수(quartile)는 자료를 동일한 비율로 4 등분 할 때의 세 위치를 말합니다.
▶ quantile( ) 함수
사분위수를 반환하는 함수입니다.
quantile(m_score)
quantile(m_score, probs = c(0.25,0.5,0.75))
▶ IQR( ) 함수
제 3 사분위수와 제 1사분위수의 차이를 반환하는 함수입니다.
IQR(m_score)
▶ boxplot( ) 함수
상자그림을 그려주는 함수입니다.
상자그림은 사분위수 시각화에 사용되는 그래프로서 자료의 주요 위치 파악과 이상점 검출 등에 사용됩니다.
boxplot(x, # 데이터
main = "Boxplot Example", # 그래프 제목
xlab = "X Values", # x축 레이블
ylab = "Y Values", # y축 레이블
col = "skyblue", # 상자 색상
notch = TRUE, # 상자의 홈 생성
horizontal = TRUE, # 가로 방향 그래프
outline = FALSE # 이상치 표시하지 않음
)boxplot(m_score,horizontal=TRUE,notch=TRUE,height=0.5,col="skyblue")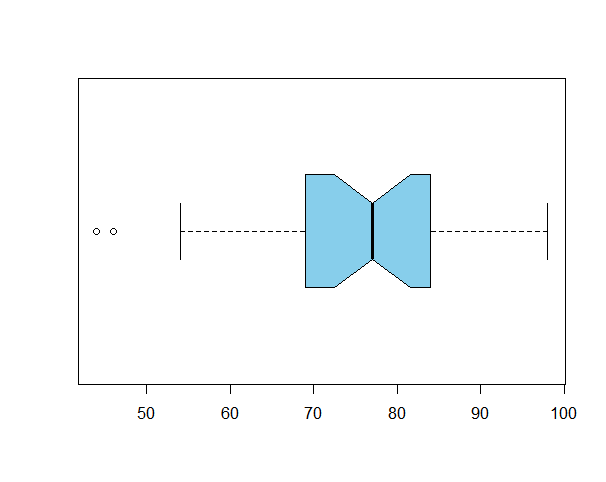
상자그림의 가운데는 데이터의 중앙 (50%)를 표현합니다. 상자(Box)의 양 끝은 데이터의 25%와 75% 지점을 나타냅니다. 수염(Whiskers) 상자 양 끝 위에 그어진 선으로 최대값과 최소값을 나타냅니다. 단 IQR의 1.5배 범위내에서 표시되며 최대값 또는 최소값이 이 범위 밖이면 이상치(outliers)로 점으로 나타냅니다. 위 자료에서 최소값은 이상치로 표시되었습니다.
4. 분산
분산의 일반식

▶ var( ) 함수
위 분산의 일반식을 계산해주는 함수입니다.
mean(m_score)
var(m_score)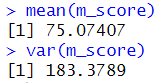
위 일반식에서 볼 수 있듯이 원래 분산을 계산하려면 평균을 구하고 각각의 관측값 차이를 제곱해서 평균을 구해야 하지만, 간단히 var( ) 함수로 분산을 구할 수 있습니다.
5. 표준편차
표준편차의 일반식

▶ sd( ) 함수
위 표준편차의 일반식을 계산해 주는 함수입니다.
sd(m_score)
6. 히스토그램(Histogram)
히스토그램은 데이터의 분포를 쉽게 파악할 수 있다는 장점이 있습니다.
상자그림은 데이터 분포의 요약정보와 이상치 감지에 사용한다면 히스토그램은 데이터 분포의 전체적인 모양과 세부구조를 파악할 대 주로 사용됩니다. 즉, 상자그림과 히스토그램을 조합하여 사용하는 것이 유용할 수 있습니다.
hist(m_score,main="수학성적분포",xlab="점수",ylab="학생수",col="skyblue")
정리
# 1. 자료불러오기
m_score <- scan()
98 75 46 80 76 65 90 85 75 54 68 78 84 96
44 78 78 68 92 85 77 56 70 80 84 72 73
# 2. 범위
range(m_score)
diff(range(m_score))
max(m_score)-min(m_score)
# 3. 사분위수
quantile(m_score)
quantile(m_score, probs = c(0.25,0.5,0.75))
IQR(m_score)
boxplot(m_score,horizontal=TRUE,notch=TRUE,height=0.5,col="skyblue")
# 4. 분산
mean(m_score)
var(m_score)
# 5. 표준편차
sd(m_score)
# 6. 히스토그램
hist(m_score,main="수학성적분포",xlab="점수",ylab="학생수",col="skyblue")'통계학 이야기' 카테고리의 다른 글
| 21. R을 이용한 표준화 - 표준점수 구하기 (0) | 2023.09.15 |
|---|---|
| 20. 수치자료의 형태 - 정규분포 (0) | 2023.09.13 |
| 18. 수치자료의 산포 - 분산, 표준편차,분위수 (0) | 2023.09.11 |
| 17. R을 이용한 수치자료의 중심 구하기 (2) | 2023.09.09 |
| 16. 수치 자료의 중심 - 평균의 한계 (0) | 2023.09.06 |




