생각 작업실 The atelier of thinking
24. 범주형 자료 요약 본문
Chapter 24. 범주형 자료 요약
1. 범주형 자료란
범주형 자료는 각각의 데이터가 명목상의 범주(category) 또는 서열상의 범주(ordinal) 중 하나에 속하는 자료를 말합니다. 명목형 자료는 분류를 목적으로 하며, 서열형 자료는 순서를 가지고 있는 범주형 자료입니다.
예를 들어, 성별, 혈액형, 종교, 결혼여부 등은 명목형 자료이고, 학년, 선호도, 군대계급 등은 서열형 자료입니다.
범주형 자료를 정리할 때 변수가 하나일 때는 도수분포표를 이용하고 변수가 2개 이상일 때는 분할표를 사용합니다.
2. 도수분포표 (Frequency Table)
(1) 도수분포표
도수분포표는 각 범주에 몇 개의 관측개체가 있는지를 정리한 표입니다.
도수는 범주에 속한 관측개체의 수를 의미합니다. (=빈도)
상대도수(relative frequency)는 전체 자료 중 해당 범주에 속한 자료의 비율을 말합니다.
◈ 예제 : 파이 판매량 자료
지난 14-1 회차 "R을 이용한 자료요약"에서 다뤘던 자료입니다.
2023.08.31 - [통계학 이야기] - 14-1. R 을 이용한 자료 요약
14-1. R 을 이용한 자료 요약
Chapter 14. R을 이용한 자료 요약 R을 이용하여 자료를 요약하는 법을 알아보겠습니다. 자료요약은 지난 11회차에 간단히 알아봤습니다. 2023.08.28 - [통계학 이야기] - 11. 자료의 요약 11. 자료의 요약
thinking-atelier.tistory.com

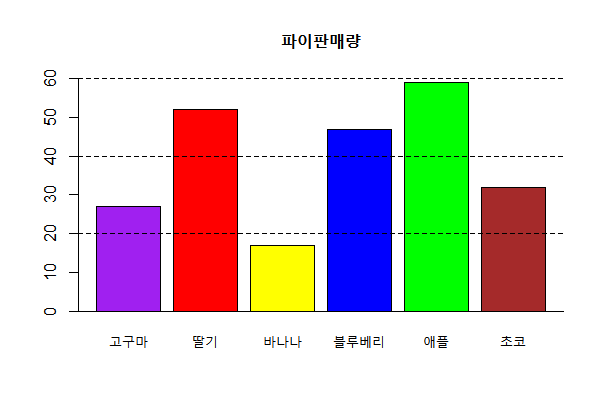
파이 판매량의 도수분포표를 위와 같이 구했습니다.
| 파이종류 | 판매량 | 판매비율(%) |
| 고구마 | 27 | 11.5% |
| 딸기 | 52 | 22.2% |
| 바나나 | 17 | 7.3% |
| 블루베리 | 47 | 20.1% |
| 애플 | 59 | 25.2% |
| 초코 | 32 | 13.7% |
위 표에 대한 시각화로 막대그래프로도 나타냈었습니다.
(2) 수치자료의 범주화
수치자료의 값이 몇 개로 한정된 경우에는 값을 범주로 처리할 수 있습니다.
구간 등을 설정하여 자료를 범주화 시키고 도수분포표를 작성할 수 있습니다.
이 때 자료는 순서자료 형태로 변환됩니다.
범주화란 계급(class)의 수와 경계값(크기)을 결정하는 것을 말합니다.
이 때 계급의 수는 자료의 특성을 고려해 분석자가 결정하며, 계급의 경계는 간격(크기)과 시작점, 끝점을 지정하고 동일간격이나 자료의 구조와 설명을 고려해 선택하게 됩니다.
3. 다변량 자료
다변량 자료란 변수가 2개 이상이라는 것을 말합니다.
통계분석 방법은 자료의 속성과 분석목적에 따라 달라지는 데 특히 다변량 자료분석과 일변량 자료분석의 다른 점은 분석 목적이라 할 수 있습니다.
다변량 자료 분석의 목적은 비교, 관계, 분류 등으로 요약해 볼 수 있습니다. 반면 일변량 자료 분석의 목적은 자료의 형태를 파악하는 것이라 할 수 있습니다. 이 때 사용하는 기술통계량은 평균, 분산 등이 대표적입니다.
다변량 자료분석에서 평균, 분산 등을 사용하는 것은 의미가 없습니다. 다만 각각의 자료에 대한 평균,분산 등을 비교해보고, 관계를 확인해보고, 분류하는 방법으로 분석하는 것이 의미있는 것이라 할 수 있습니다.
다변량 자료의 형태는 아래와 같이 구분해 볼 수 있습니다.
| 경우 | X | Y |
| (1) | 범주형 자료 | 범주형 자료 |
| (2) | 범주형 자료 | 수치형 자료 |
| (3) | 수치형 자료 | 범주형 자료 |
| (4) | 수치형 자료 | 수치형 자료 |
다변량 자료의 분석목적은 아래와 같이 요약할 수 있습니다.
(1) 비교 : X에 따라 Y에 차이가 있는가 ?
(2) 관계 : X와 Y가 관련이 있는가? 혹은 X가 Y에 영향을 주는가?
(3) 분류 : X에 따라 Y를 분류할 수 있는가? 혹은 X,Y가 비슷한 것끼리 묶을 수 있는가?
4. 분할표(Contingency Table)
두 개 이상의 변수를 동시에 고려하여 각각의 범주에 관측개체의 빈도를 정리한 교차표(cross tabulation)입니다.
◈ 예제 : 세 가지 스마트폰 모델에 대한 남녀별로 선호도 비교
이 예제의 분석목적은 둘 다 범주자료일 때 비교하고자 합니다.
위 자료 146 명에 대한 선호도 조사결과를 아래의 분할표로 정리해 볼 수 있습니다.
| 성별 | 스마트폰 모델 | 합계 | ||
| A | B | C | ||
| 남자 | 35 | 23 | 18 | 76 |
| 여자 | 17 | 33 | 20 | 70 |
| 합계 | 52 | 56 | 38 | 146 |
위 자료는 남자 76명과 여자 70명을 대상으로 세 가지 모델(A,B,C) 중 가장 마음에 드는 모델을 선택한 조사 결과 입니다.
결과를 살펴보면 남자 중 모델 A는 35, B는 23, C는 18명이 선택하고 여자 중 A는 17명, B는 33명, C는 20명이 선택하였습니다.
위 자료 분석을 위하여 비율(상대도수)을 표시하려고 할 때, 분석 목적 또는 자료가 어떻게 수집되었는지에 따라 비율은 다르게 나타납니다. 즉, 기준(분모)를 어떻게 할 것이냐에 따라 다르게 나타납니다.
(1) 기준(분모)를 무작위로 한 경우 (전체 합이 분모로 했을 때)
| 성별 | 스마트폰 모델 | 합계 | ||
| A | B | C | ||
| 남자 | 35 (24.0%) |
23 (15.8%) |
18 (12.3%) |
76 (52.1%) |
| 여자 | 17 (11.6%) |
33 (22.6%) |
20 (13.7%) |
70 (47.9%) |
| 합계 | 52 (35.6%) |
56 (38.4%) |
38 (26.0%) |
146 (100%) |
위 분할표를 보면 유의미한 연관성이 눈에 쉽게 띄이지 않습니다.
(2) 분석목적이 성별에 따른 모델 선호도일 때 (분모가 각 성별 합계 일 때)
| 성별 | 스마트폰 모델 | 합계 | ||
| A | B | C | ||
| 남자 | 35 (46.0%) |
23 (30.3%) |
18 (23.7%) |
76 (100%) |
| 여자 | 17 (24.3%) |
33 (47.1%) |
20 (28.6%) |
70 (47.9%) |
| 합계 | 52 (35.6%) |
56 (38.4%) |
38 (26.0%) |
146 (100%) |
성별에 따른 모델 선호 비율을 비교해 볼 수 있습니다.
남성은 A 모델을, 여성은 B 모델을 가장 선호한다는 것을 알 수 있습니다.
이 분석결과를 마케팅에 적용한다면, 남성에게는 A 모델을, 여성에게는 B 모델을 중점으로 하는 전략을 취할 수 있을 겁니다.
위 분할표를 시각화를 해보겠습니다.
5. 그래프로 표현하기
앞서 유의미한 결과를 보여주는 성별에 따른 모델 선호도에 대하여 그래프로 나타내 보겠습니다.
(1) 남성이 선호하는 모델 분석
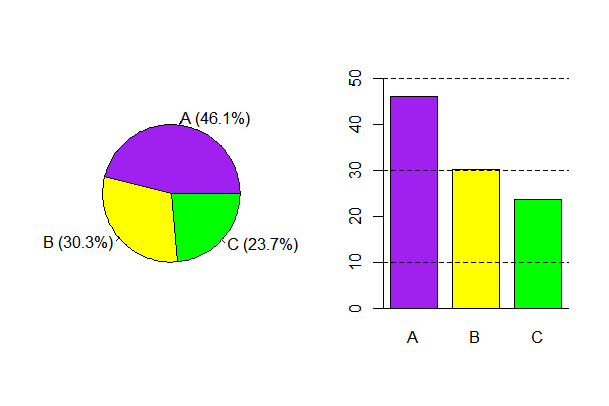
그래프로 보면 위 분할표에 비해 직관적으로 모델 A의 선호도가 가장 높다는 것을 쉽게 인지할 수 있습니다.
(2) 여성이 선호하는 모델

여성의 경우 모델 B에 대한 선호도가 가장 높다는 것을 인지할 수 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 26. 다변량 자료의 기술 통계 - 공분산, 상관관계 & 산점도 (0) | 2023.09.22 |
|---|---|
| 25. R을 이용한 범주형 자료 요약 (2) | 2023.09.21 |
| 23. R을 이용하여 왜도, 첨도 구하기 (0) | 2023.09.19 |
| 22. 수치자료의 형태 - 왜도, 첨도 (0) | 2023.09.18 |
| 21. R을 이용한 표준화 - 표준점수 구하기 (0) | 2023.09.15 |





