생각 작업실 The atelier of thinking
26. 다변량 자료의 기술 통계 - 공분산, 상관관계 & 산점도 본문
Chapter 26. 다변량 자료의 기술통계
앞서 다변량 변수(자료) 형태는 아래와 같이 나눠봤습니다.
| 경우 | X | Y |
| (1) | 범주형 자료 | 범주형 자료 |
| (2) | 범주형 자료 | 수치형 자료 |
| (3) | 수치형 자료 | 범주형 자료 |
| (4) | 수치형 자료 | 수치형 자료 |
1. 산점도(Scatter Plot)
다변량 자료의 분석목적이 "관계"에 대한 분석도구로 가장 많이 사용되는 것은 산점도와 상관계수입니다.
두 변수의 값을 각각 x축과 y축을 이용하여 표시나 그림을 산점도(Scatter Plot)라고 합니다.
(1) 자료구조와 분석목적
▶ 구조 : 수치자료 + 수치자료(+...+수치자료)
각각의 관측개체에 대해 두 변수의 값은 순서쌍(x,y)...으로 표시
▶ 목적 : 수치 변수들 간의 관계를 유도 순서쌍 자료를 2차원 평면상에 점으로 표시한 그림
◈ 예제 : 올림픽 100미터 우승 기록
| 연도 | 우승기록 | 연도 | 우승기록 | 연도 | 우승기록 | |||
| 남자 | 여자 | 남자 | 여자 | 남자 | 여자 | |||
| 1896 | 12 | - | 1936 | 10.3 | 11.5 | 1988 | 9.92 | 10.54 |
| 1900 | 11 | - | 1948 | 10.3 | 11.9 | 1992 | 9.96 | 10.82 |
| 1904 | 11 | - | 1952 | 10.4 | 11.5 | 1996 | 9.84 | 10.94 |
| 1908 | 10.8 | - | 1956 | 10.5 | 11.5 | 2000 | 9.87 | 10.75 |
| 1912 | 10.8 | - | 1960 | 10.2 | 11.0 | 2004 | 9.85 | 10.93 |
| 1920 | 10.8 | - | 1964 | 10.0 | 11.4 | 2008 | 9.69 | 10.78 |
| 1924 | 10.6 | - | 1968 | 9.9 | 11.0 | 2012 | 9.63 | 10.75 |
| 1928 | 10.8 | 12.2 | 1976 | 10.14 | 11.07 | 2016 | 9.81 | 10.71 |
| 1932 | 10.3 | 11.9 | 1984 | 10.06 | 10.97 | |||
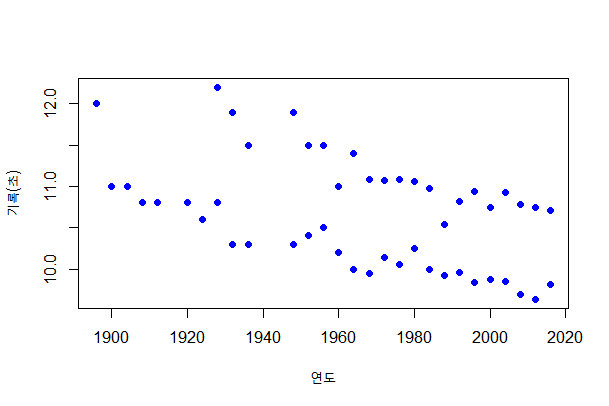
위 산점도는 연도와 기록간의 관계를 보여줍니다.
2. 상관계수(codfficient of correlation)와 공분산(covariance)
(1) 상관계수의 필요성

위 두 산점도는 가로든 세로든 중심과 퍼진 정도는 동일하지만 왼쪽 그림이 더 강한 선형관계를 보이고 있습니다.
두 변수간 선형관계의 방향과 강도가 얼마나 되는지 측정할 필요성이 대두됩니다.
상관계수와 공분산는 두 변수간 관계를 나타내는 통계적인 지표입니다.
(2) 공분산 (Covariance)
공분산은 두 변수 사이의 관계를 나타내는 지표 중 하나로, 두 변수의 함께 움직이는 경향을 측정합니다.
공분산의 수식은,

양과 음의 관계를 가지는 산점도

공분산의 부호는 두 변수 간의 관계를 나타냅니다.
양수 공분산(왼쪽) : 두 변수가 함께 증가 또는 감소하는 경향이 있음을 나타냅니다.
음수 공분산(오른쪽) : 하나의 변수가 증가할 때 다른 변수가 감소하는 경향이 있음을 나타냅니다.
공분산이 0에 가까울수록 두 변수 간의 선형관계가 약하거나 없음을 나타냅니다.
공분산의 문제점은 측정 단위에 영향을 받기 때문에 그 값 자체로 선형관계의 정도를 알 수는 없다는 점입니다.
(3) 상관계수 (Correlation Coefficient)
상관계수는 앞선 공분산의 문제점을 보완하고자 고안된 것입니다.
상관계수는 두 변수간의 선형관계의 강도와 방향을 나타내는 지표입니다. 상관계수는 -1에서 1사이의 값을 가지며, 다음과 같은 수식으로 정의할 수 있습니다.
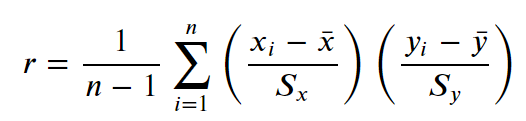
상관계수는 공분산을 각 변수의 표준편차로 나눈 것이므로 단위에 영향을 받지 않습니다. 따라서 상관계수는 두 변수간의 선형관계를 정규화한 지표로 다양한 변수 간의 관계를 비교하는 데 유용합니다.
즉, 공분산은 두 변수의 단위에 의존하고, 상관계수는 단위에 독립적으로 두 변수 간의 관계를 측정하는 지표입니다. 관계적인 개념으로 공분산은 상관계수의 원시형태로 볼 수 있습니다.
공분산은 두 변수가 어떻게 함께 움직이는지를 알려주고,
상관계수는 두 변수가 얼마나 관련이 있는지를 알려준다고 할 수 있습니다.
(4) 상관계수의 한계
아래의 그래프는 모두 다른 모양이지만 같은 상관계수 0.816 을 나타냅니다.

아래의 그래프는 모두 비선형으로 상관계수가 0을 나타냅니다.
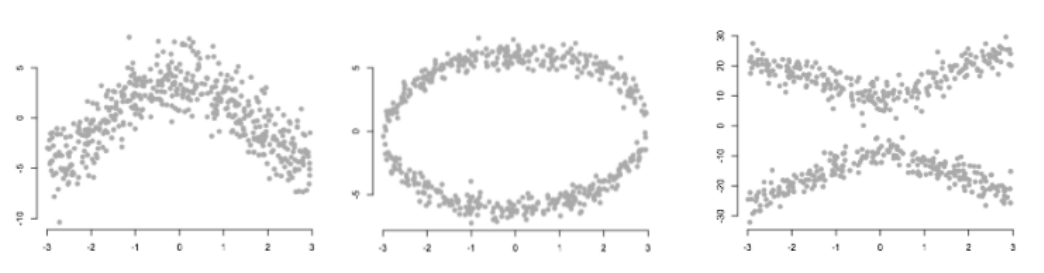
위 그래프에서 보듯이, 선형일 때만 상관관계/공분산이 유용하며 상관계수가 측정할 수 있는 것은 선형관계일 때만 가능합니다.
(5) 상관계수 사용 시 주의할 점
상관계수는 두 변수간에 직선관계가 있는지를 나타낼 뿐 인과관계를 나타내는 것은 아니다.
예를 들어, 휴대전화 보급률과 기대수명에 대한 상관계수는 매우 높은 양의 상관관계를 가진다고 합니다. 하지만, 기대수명을 늘리기 위해 휴대전화 보급을 늘려야 할까요?
잠복변수(lurking variable)는 두 변수에 영향을 주는 변수입니다.
위 경우의 잠복변수는 연도(시간의 흐름)가 휴대전화 보급률을 늘려주고 기대 수명을 높여주는 것일 수 있습니다.
이 때 휴대전화 보급률과 기대수명 증가 사이의 관계는 허위상관(spurious correlation)이라 합니다.
보급률과 기대수명에서 연도의 영향력을 제거하고 상관관계를 유도해야 보다 정확한 관계를 얻을 수 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 28. 확률과 통계 (0) | 2023.09.26 |
|---|---|
| 27. R을 이용한 산점도, 공분산, 상관관계 구하기 (0) | 2023.09.25 |
| 25. R을 이용한 범주형 자료 요약 (2) | 2023.09.21 |
| 24. 범주형 자료 요약 (0) | 2023.09.21 |
| 23. R을 이용하여 왜도, 첨도 구하기 (0) | 2023.09.19 |




