생각 작업실 The atelier of thinking
30. 확률과 경우의 수(The Number of Cases) 본문
Chapter 30. 확률과 경우의 수
1. 경우의 수
확률을 계산하기 위해서는 표본공간과 사건에 있는 원소의 갯수를 효율적으로 계산하는 것이 중요합니다. 즉, 표본공간의 크기와 사건의 크기를 알아내는 것이 필요합니다.
경우의 수는 어떤 사건이나 실험에서 일어날 수 있는 모든 가능한 경우의 개수를 나타냅니다. 간단히 말하면, 특정 상황에서 발생 가능한 다양한 선택 또는 결과의 수를 의미합니다.
경우의 수를 알면 각 결과가 일어날 확률을 계산할 수 있으며, 이를 통해 다양한 확률적 문제를 해결할 수 있습니다.
경우의 수를 구하는 기본 법칙은 곱의 법칙(multiplication rule) 입니다.
곱의 법칙이란 예를 들어 어떤 실험이 m 개의 연속된 단계로 이루어져 있고,
i 번째 단계에서 발생가능한 결과의 수를 ni라 한다면,
전체 실험에서 발생 가능한 경우의 수는,
각 단계의 경우의 수를 모두 곱하는 것을 말합니다.
◈ 예제 : 세트 메뉴 선택하기
세트메뉴에는 4 가지 음료수, 2 가지 샐러드, 5 가지 메인, 4가지의 디저트 중에서 각각 하나씩을 선택한다고 했을 때,
선택할 수 있는 세트의 종류는
4 X 2 X 5 X 4 = 160
총 경우의 수는 160 가지 조합이 나옵니다.
◈ 예제 : 두 개의 주사위를 던져 나오는 경우의 수
6 X 6 = 36 , 36이 나옵니다.

2. 추출방법 및 배열 방법에 따른 경우의 수
예를 들어 아래의 주머니에서 1번 부터 4번까지 적혀있는 공을 무작위로 2개를 선택한다고 했을 때,

(1) 추출방법
복원추출은 첫번째 공을 뽑은 후 다시 주머니에 공을 넣고 두번째 공을 뽑는 것을 말합니다.

비복원추출은 첫번째 공을 뽑은 후 다시 주머니에 공을 넣지 않고 남은 공들 중에서 두번째 공을 뽑는 것을 말합니다.

또한 한꺼번에 두 개를 뽑는다고 하면, 중복이 없기 때문에 비복원추출이라고 할 수 있습니다.
(2) 배열 방법
추출한 공의 순서를 고려하는 여부에 따라 경우의 수는 다르게 나타납니다.
순서를 고려한다면, (1,2) 와 (2,1)은 다른 것으로 경우의 수는 2 입니다.
순서를 고려하지 않는다면, (1,2)와 (2,1)은 같은 것으로 경우의 수는 1 입니다.
3. 경우의 수 분류
추출방법과 배열 방법에 따라 아래와 같이 분류해 볼 수 있습니다.
| 배열 / 추출 | 복원 | 비복원 |
| 순서고려 | 중복순열 | 순열 Permutation |
| 순서무시 | 중복조합 | 조합 Combination |
이렇게 분류하는 이유는 추출방법과 순서고려 여부에 따라 계산하는 방법이 각각 다르기 때문입니다.
(1) 중복순열 : 복원 추출 + 순서고려
복원추출이고 순서를 고려할 때의 각 회차별 경우의 수는 처음부터 끝까지 모두 같습니다.
1회차의 경우의 수는 n이고, 2회차의 경우의 수도 n, 그리고 k 회차 경우의 수도 n 입니다.
따라서 전체 경우의 수는 n을 k 번 반복하여 곱해주면 됩니다.
수식은 아래와 같이 표현합니다.
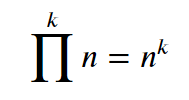
(2) 순열(permutation) : 비복원추출 + 순서고려
비복원추출이므로 1회차의 경우의 수는 n, 2회차의 경우의 수는 n-1, k회차의 경우의 수는 n-k+1이 됩니다,
전체 경우의 수는 각 경우의 수를 곱해주면 됩니다. 즉, n X (n-1) X ...X (n-k+1) 입니다.
이 수식을 간략하게 표현하면,

혹은,

이 수식에 이르는 과정은 아래와 같습니다.

위 n X (n-1) X ...X (n-k+1) 에 (n-k)!/(n-k)! 를 곱하면 분자는 n! , 분모는 (n-k)!로 정리할 수 있습니다.
(3) 조합(combination) : 비복원추출 + 순서무시
조합은 비복원추출이므로 경우의 수는 순열의 경우를 적용할 수 있습니다.
순서를 무시하기 때문에 순열의 경우의 수에서는 다른 것으로 분류하지만 조합에서는 같은 것으로 분류하게 됩니다. 따라서 k! 만큼을 더 나누어줘야 합니다.
수식으로는,

(4) 중복조합 : 복원추출 + 순서무시
조합이 순열에서 k! 만큼 나누어 구한 것처럼, 중복조합을 구할 때 중복순열에서 k! 만큼 나누면 될 것 같지만, 이렇게 하면 오류가 발생합니다. 오류가 발생하는 이유는 중복순열과 나눌 대상이 되는 분자부분의 경우의 수가 다르기 때문입니다.
예를 들어, 4개의 구슬 중 3 개를 복원추출 한다고 할 때, 아래의 그림처럼 4개의 칸에 구슬을 하나씩 넣는다고 했을 때,
1번째 경우의 수는 4 가 됩니다.

2번째 경우의 수는 중복순열이라면 4가 되어야 하지만, 순서를 고려해야한다면,

위 그림처럼 2번칸에 들어가 있는 구슬의 앞과 뒤가 다른 경우의 수가 되므로, 이 때의 경우의 수는 5가 됩니다.
같은 이유로 3번째 경우의 수는 6이 됩니다.

따라서, 총 경우의 수는 4 X 5 X 6 이 됩니다.
이를 일반화하면, n+k-1에서 k개 조합을 구하는 것이라 볼 수 있습니다. 따라서, 수식은 아래와 같습니다.

아래 예제를 통하여 중복순열,순열,조합,중복조합에 따른 각각의 경우의 수를 구해보겠습니다.
◈ 예제 : 주머니 안에 있는 공 4 개에서 3개를 선택할 때
즉 n = 4 , k = 3 일 때,
(1) 중복순열 - 복원 + 순서 일때
1번째 경우의 수 : 4 , 2번째 경우의 수 : 4 , 3번째 경우의 수 : 4
따라서, 4 X 4 X 4 = 64
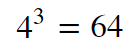
총 64의 경우의 수를 가집니다.
(2) 순열 - 비복원 + 순서

총 24의 경우의 수를 가집니다.
(3) 조합 - 비복원 + 순서X
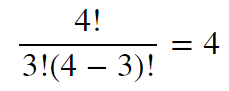
총 4 의 경우의 수를 가집니다.
(4) 중복조합 - 복원 + 순서X

총 20의 경우의 수를 가집니다.
'통계학 이야기' 카테고리의 다른 글
| 32. 고전적 확률 vs. 조건부 확률 (1) | 2023.10.11 |
|---|---|
| 31. R을 이용한 경우의 수 구하기 (1) | 2023.10.09 |
| 29. 확률의 공리와 기본 정리 (1) | 2023.09.27 |
| 28. 확률과 통계 (0) | 2023.09.26 |
| 27. R을 이용한 산점도, 공분산, 상관관계 구하기 (0) | 2023.09.25 |




