| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 경제학
- 정규분포
- 이항분포
- 티스토리챌린지
- 에세이
- 산점도
- 이원배치 분산분석
- 확률
- 변량효과모형
- 추정
- 반복없음
- version 1
- 반복있음
- 고정효과모형
- 가설검정
- css
- 데이터 과학
- 해운업
- JavaScript
- 인공지능
- 분산분석
- html
- version 2
- 혼합효과모형
- 오블완
- 회귀분석
- 통계학
- r
- 변동분해
- 글쓰기
- Today
- Total
생각 작업실 The atelier of thinking
32. 고전적 확률 vs. 조건부 확률 본문
Chapter 32. 고전적 확률 vs 조건부 확률
1. 확률의 기원
슈발리에 드 메레 (Chevalier de Mere)의 질문에서 시작되엇다고 합니다. 1650년대 프랑스 작가 슈발리에 드 메레는 다음과 같은 도박 문제를 고심하고 있었다고 합니다.
- 게임 1 : 최대 4번까지 공정한 주사위를 한 개 던지는데 6이 나오면 이긴다.
- 게임 2 : 최대 24번까지 공정한 주사위를 두 개 던지는데 둘 다 6이 나오면 이긴다.
과연 어느 게임이 더 유리한 게임일까요?
이 문제에 대한 해답을 구하기 위해 드 메레가 도움을 청한 사람은 파스칼이었고, 파스칼은 그의 친구 페르마와 같이 확률론의 기반을 다지게 되었다고 합니다. 각 게임의 확률을 구해보면 아래와 같습니다.
(1) 게임 1 : 최대 4번까지 공정한 주사위를 한 개 던지는데 6이 나오면 이긴다.
여사건의 법칙에 따라 게임 1의 승률은 "1 - (4번 모두 6 이외의 숫자가 나올 확률)" 로 계산할 수 있습니다.
여기서 각각 주사위를 던질 때 나오는 눈의 개수는 서로 영향을 주지 않으므로 곱셈의 법칙을 사용하여 (4번 모두 6 이외의 숫자가 나올 확률)은 (모두 6 이외의 숫자가 나올 확률)을 4번 곱해서 구할 수 있습니다.
아래의 계산에 따라 게임 1의 승률은, 51.77% 입니다.

(2) 게임 2 : 최대 24번까지 공정한 주사위를 두 개 던지는데 둘 다 6이 나오면 이긴다.
여사건의 법칙에 따라 게임 2의 승률은 "1 - (24번 모두 둘 다 6 이 나오지 않을 확률)" 로 계산할 수 있습니다.
여기서 둘 다 6이 나오지 않을 확률은 1 - (1/6 X 1/6) = 35/36 입니다.
아래의 계산에 따라 게임 2의 승률은, 49.14% 입니다.

2. 고전적 확률
고전적 확률은 주사위 던지기와 동전 던지기와 같이 모든 결과가 나올 확률이 동일하다는 전제하에 특정 사건이 나올 확률을 계산합니다.
가정 : 표본공간의 각 원소(근원사건)의 발생가능성이 동일(equally likely)하다.
- n : 표본공간의 원소개수
- k : 사건 A의 원소개수
- 사건 A의 확률 :

발생 가능성이 동일하다는 전제가 중요포인트입니다. 빈도확률이라 부릅니다.
위 표본공간의 원소 개수와 사건 A의 원소 개수를 구할 때는 앞서 언급하였던 경우의 수를 사용하게 됩니다.
3. 조건부 확률
조건부 확률(conditional probability)이란 확률실험에서 새로운 정보 또는 조건(A)이 추가 되었을 대, 사건 B의 확률을 말합니다. 여기서 정보 또는 조건은 광범위한 표본 공간을 좁혀주는 (narrow down) 역할을 합니다.
경험적 확률이라고도 불립니다. 정보와 조건은 과거 경험과 현재 상황을 고려해서 나오기 때문입니다.

위 그림에서 사건 A가 발생했다면 A 이외의 것은 일어날 수 없습니다.
즉 A가 새로운 표본공간이 되고 B가 발생한다는 것은 A와 B의 교집합에 있는 원소가 발생하는 것을 의미합니다.
사건 A가 주어졌을 때 사건 B의 조건부 확률을 식으로 표현하면,
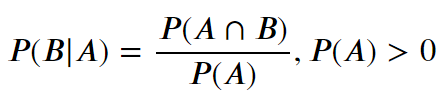
4. 고전적 확률과 조건부 확률의 차이점
고전적 확률과 조건부 확률은 확률 계산의 기본적인 접근 방식에서 차이가 있습니다.
고전적 확률은 이론적인 확률로 균일한 조건 아래에서 각 사건의 확률을 계산하는 방법입니다.
각 사건이 발생할 가능성이 동일하다고 가정합니다. 공정한 주사위나 동전 던지기와 같이 각 결과가 동일한 확률을 가질 때 적용됩니다.
반면 조건부 확률은 특정 조건 아래에서 사건의 확률을 계산하는 방법입니다. 이전 사건이 발생했다는 조건 하에 새로운 사건이 발생할 확률을 계산합니다. 즉 조건부 확률은 주어진 조건에서 사건 A가 발생할 확률을 나타냅니다.
고전적 확률은 이론적으로 가능한 결과의 수를 전체 가능한 결과의 수로 나누어 계산하는 것에 중점을 두며, 각 결과가 동일한 확률을 가정합니다. 반면 조건부 확률은 이전 사건이 발생했다는 조건 하에 새로운 사건의 확률을 계산하는 것에 중점을 둡니다. 이는 특정 상황에서의 확률을 고려하여 계산하는 더 유연한 방법입니다.
'통계학 이야기' 카테고리의 다른 글
| 34. 조건부 확률 - 베이즈 정리의 활용 (0) | 2023.10.13 |
|---|---|
| 33. 조건부 확률 - 베이즈 정리(Bayes' theorem) (0) | 2023.10.12 |
| 31. R을 이용한 경우의 수 구하기 (0) | 2023.10.09 |
| 30. 확률과 경우의 수(The Number of Cases) (1) | 2023.10.08 |
| 29. 확률의 공리와 기본 정리 (1) | 2023.09.27 |




