생각 작업실 The atelier of thinking
39. 확률분포 - 결합분포&주변분포 본문
Chapter 39. 확률분포-결합분포&주변분포
1. 결합분포(Joint Distribution)
결합분포는 두 개 이상의 확률변수에 대한 확률분포를 말합니다.
즉, 각각의 변수가 어떤 값을 가질 때 어떤 사건이 일어날 확률을 나타내는 함수입니다.
예를 들어, 두 개의 확률변수 X와 Y를 ( X,Y )로 나타낸다면, 결합분포는 P ( X=x, Y=y )로 표현합니다.
이러한 결합분포는 각 변수의 확률분포를 알면 쉽게 구할 수 있습니다.
결합분포는 두 변수 간의 상관관계를 분석하는데 사용됩니다.
결합분포를 나타내는 확률함수 역시 이산확률변수와 연속확률변수 일 때로 구분하여 각각 결합확률질량함수, 결합확률밀도함수라고 말합니다.
(1) 결합확률질량함수(Joint Probability Mass Function) - 이산확률변수
결합확률질량함수는 이산형 확률변수들에 대해 사용되며, 각각의 확률변수가 가질 수 있는 값의 조합에 대한 확률값을 나타냅니다.
두 이산 확률변수 X와 Y에 대한 결합확률질량함수는 아래와 같이 표현합니다.
$$ f( x,y ) = P(X=x,Y=y) = P(X=x and Y=y) $$
n개의 이산확률변수에 대해서는 아래와 같이 표현할 수 있습니다.
$$ f(x_1,x_2, ... ,x_n) = P(X_1=x_1, X_2=x_2, ... ,X=x_n) $$
◈ 예제 : 동전 3 개 던지기
동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 입니다.
앞면이 나오는 확률변수 X의 값은 0,1,2,3 으로 나타납니다.
앞면과 뒷면의 수 차이는 확률변수 Y의 값은 1,3 으로 나타납니다.
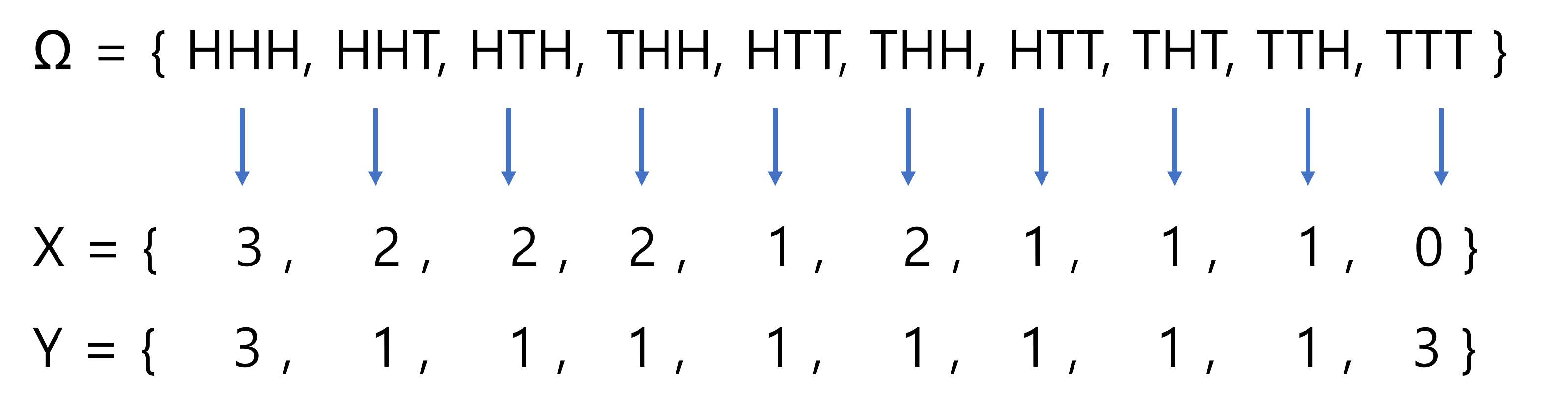
결합확률질량함수로 표현하면,
$$ f(0,3) = \frac{1}{8} , f(1,1) = \frac{3}{8}, f(2,1) = \frac{3}{8}, f(3,3) = {1}{8} $$
이를 표로 정리하면,
| Y \ X | 0 | 1 | 2 | 3 |
| 1 | 0 | $ \frac{3}{8} $ | $ \frac{3}{8} $ | 0 |
| 3 | $ \frac {1}{8} $ | 0 | 0 | $ \frac {1}{8} $ |
이 때 결합확률질량함수의 특징은 0과 1 사이의 값을 갖습니다. 그리고 함수의 합은 1 입니다.
$$ 0 \leq f(x,y) \leq 1 , \forall x,y $$
$$ \begin{align} \sum_{x}\sum_{y}f(x,y) = 1\end{align}$$
(2) 결합확률밀도함수(Joint Probability Density Function) - 연속확률변수
결합확률밀도함수는 연속형 확률변수들에 대해 사용되며, 결합확률밀도함수값이 두 변수의 구간에서 적분한 값은 해당 구간에서의 결합확률을 나타냅니다.
두 연속 확률변수 X와 Y에 대한 결합확률밀도함수 f(x,y)는 x,y에서의 밀도(높이)를 나타내며 아래의 성질을 만족합니다.
$$ 0 \leq f(x,y) $$
$$ \int_{x} \int_{y} f(x,y) = 1 $$
부피 = 1 이고 밀도는 음수를 나타낼 수 없기 때문에 0보다 크거나 같습니다.
◈ 예제 : 균일분포(균등분포) - Uniform Distribution
균일분포란 정해진 범위에서 모든 확률이 균일한 분포를 말합니다. (통계학의 가장 기본이 되는 분포입니다.)
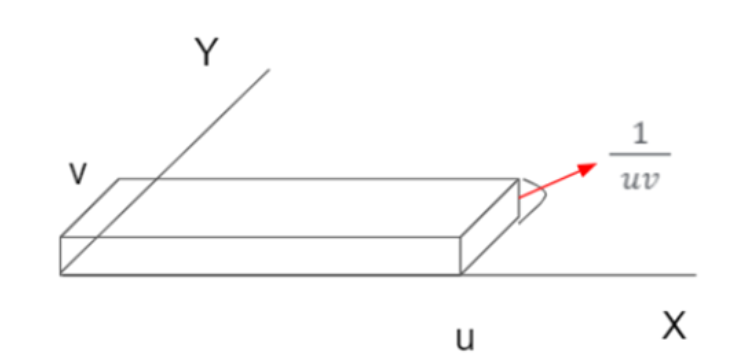
균일분포 (X,Y) ~ U ( (0,u), (0,v)) 의 결합확률밀도함수는,
$$ f(x,y) = \frac{1}{uv} , 0 < x < u, 0 < y < v $$
이것을 그림으로 표현하면,
2. 주변분포 (Marginal Distribution)
주변분포란 그 부분집합에 속한 확률변수들의 확률분포를 뜻합니다.
이는 다른 확률 변수의 값을 무시한 부분 집합 속의 확률 변수의 분포를 알 수 있게 해줍니다. 이는 조건부 확률과 대비되는 부분입니다.
결합확률분포에서 한 확률변수에 대한 확률분포를 구할 때 사용하는 것이 주변분포입니다.
주변분포는 결합분포에서 원하는 하나의 확률변수를 선택하고, 나머지 확률변수에 대해서는 모든 가능한 값들의 합 또는 적분을 통해 구할 수 있습니다. 이렇게 구한 확률분포는 선택된 확률변수 하나에 대한 확률분포입니다.
예를 들어, (X,Y)의 결합분포가 주어졌을 때, X에 대한 주변분포를 구하고 싶다면, 모든 가능한 Y값에 대한 확률을 더하거나 적분하여 X의 분포를 구할 수 있습니다. Y에 대한 주변분포도 마찬가지로 모든 가능한 X 값에 대한 확률을 더하거나 적분하여 구할 수 있습니다.
주변분포는 결합분포에서 원하는 확률변수에 대한 정보를 얻기위해 사용되며, 다변량 확률론에서 중요한 개념 중 하나입니다.
(1) 주변확률질량함수(Marginal Probability Mass Function) - 이산확률변수
주변확률질량함수는 결합확률질량함수에서 하나의 확률변수에 대한 확률분포를 구할 때 사용하는 확률함수입니다.
앞서 분할(Partition)은 합쳐서 전체를 포괄하되 겹쳐서 중복이 안되는 사건들의 집합이라 했습니다.
이 분할을 통해서 주변확률질량함수를 유도하면 아래와 같습니다.
표본공간이 사건 $ B_1, B_2, ... , B_n $ 으로 분할 될 때 사건 A의 확률은,
$$ P(A) = P(A \cap B_1)+P(A \cap B_2)+ ... +P(A \cap B_n)=\sum_{i=1}^n P(A \cap B_i) $$
위의 식에서 사건 A 를 $ X=x $ 로 $ B_i = y_i $ 라고 가정하면,
$$ P(A \cap B_i) = P( X=x, Y=y_i) = f(x,y_i) $$
따라서, P(X=x)를 구하는 식은,
$$ P(X=x) = P(A) = \sum_{i=1}^n P(A \cap B_i) = \sum_{i=1}^n P(X=x, Y=y_i) $$
$$ f_X(x) = \sum_{y} f(x,y) $$
Y=y에 대한 식은,
$$ f_Y(y) = \sum_{x} f(x,y) $$
$f_X(x)$ : X의 주변확률질량함수
$f_Y(y)$ : Y의 주변확률질량함수
◈ 예제 : 동전 3 개 던지기
동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 입니다.
앞면이 나오는 확률변수 X의 값은 0,1,2,3 으로 나타납니다.
앞면과 뒷면의 수 차이는 확률변수 Y의 값은 1,3 으로 나타납니다.
앞서 결합확률분포는
| Y \ X | 0 | 1 | 2 | 3 |
| 1 | 0 | $ \frac{3}{8} $ | $ \frac{3}{8} $ | 0 |
| 3 | $ \frac {1}{8} $ | 0 | 0 | $ \frac {1}{8} $ |
여기에 주변확률질량함수를 표시하면,
$$ f_X(0) = \frac{1}{8} , f_X(1) = \frac{3}{8}, f_X(2) = \frac{3}{8}, f_X(3) = \frac{1}{8} $$
$$ f_Y(1) = \frac{6}{8} = \frac{3}{4} , f_Y(3) = \frac{2}{8} = \frac{1}{4} $$
이를 표로 나타내면,
| Y \ X | 0 | 1 | 2 | 3 | $ f_Y $ |
| 1 | 0 | $ \frac{3}{8} $ | $ \frac{3}{8} $ | 0 | $ \frac{3}{4} $ |
| 3 | $ \frac {1}{8} $ | 0 | 0 | $ \frac {1}{8} $ | $ \frac{1}{4} $ |
| $ f_X $ | $ \frac {1}{8} $ | $ \frac{3}{8} $ | $ \frac{3}{8} $ | $ \frac {1}{8} $ | 1 |
(2) 주변확률밀도함수(Marginal Probability Density Function) - 연속확률변수
결확확률밀도함수를 통해 얻은 다변수 확률분포에서 한 변수의 확률분포를 구하는 것이 주변확률밀도함수 입니다.
$$ f_X(x) = \int f(x,y) dy $$
$$ f_Y(y) = \int f(x,y) dx $$
◈ 예제 : 균일분포(균등분포) - Uniform Distribution
균일분포 (X,Y) ~ U ( (0,u), (0,v)) 의 결합확률밀도함수는,
$$ f(x,y) = \frac{1}{uv} , 0 < x < u, 0 < y < v $$
$$ f_X(x) = \int_{0}^v \frac{1}{uv}dy = \frac{1}{uv} [y]_{0}^v=\frac{1}{u}, 0<x<u $$
$$ f_Y(y) = \int_{0}^v \frac{1}{uv}dx = \frac{1}{uv} [x]_{0}^u=\frac{1}{v}, 0<y<v $$
3. 독립확률변수
독립확률변수란 두 확률변수의 결합분포가 주변확률분포의 곱과 같아지는 확률변수를 의미합니다. 즉, 하나의 확률변수가 다른 확률변수의 값을 예측하는 데 전혀 도움이 되지 않는 경우를 의미합니다.
독립확률변수 X와 Y가 있다면, X가 어떤 값을 갖더라도 Y의 분포에는 영향을 미치지 않고, Y가 어떤 값ㅇ르 갖더라도 X의 분포에는 영향을 미치지 않습니다. 따라서, 두 변수의 공분산은 0이 되며, 독립성은 상관계수가 0이 되는 것으로 나타낼 수 있습니다.
독립확률변수는 다변량 확률분포와 조건부 확률 등의 개념에서 사용됩니다.
사건 A와 사건 B가 독립일 때, $ P(A \cap B) = P(A) P(B) $ 임을 두 확률변수 X와 Y는 독립이라는 것에 적용하면, 모든 x,y에 대해 독립이라는 의미로 아래와 같이 표현할 수 있습니다.
$$ f(x,y) = f_X(x) f_Y(y) $$
따라서, n개의 확률변수가 독립이라는 것은 아래와 같이 표현할 수 있습니다.
$$ f(x_1,x_2, ... ,x_n) = f_{X_1}(x_1) f_{X_2}(x_2) ... f_{X_n}(x_n) = \prod_{i=1}^n f_X(x_i) $$
◈ 예제 : 동전 3 개 던지기
동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 입니다.
앞면이 나오는 확률변수 X의 값은 0,1,2,3 으로 나타납니다.
앞면과 뒷면의 수 차이는 확률변수 Y의 값은 1,3 으로 나타납니다.
| Y \ X | 0 | 1 | 2 | 3 | $ f_Y $ |
| 1 | 0 | $ \frac{3}{8} $ | $ \frac{3}{8} $ | 0 | $ \frac{3}{4} $ |
| 3 | $ \frac {1}{8} $ | 0 | 0 | $ \frac {1}{8} $ | $ \frac{1}{4} $ |
| $ f_X $ | $ \frac {1}{8} $ | $ \frac{3}{8} $ | $ \frac{3}{8} $ | $ \frac {1}{8} $ | 1 |
위 표에서 $f(1,1) = \frac{3}{8}, f_X(1) = \frac{3}{8}, f_Y(1) = \frac{3}{4} $ 를 알 수 있습니다.
$$ f(1,1) \not= f_X(1) f_Y(1) $$
독립인 경우는 $ f(x,y) = f_X(x) f_Y(y) $ 이므로 위 경우 X와 Y는 독립이 아닙니다.
◈ 예제 : 독립인 경우
$$ f(x,y) = \frac{xy}{36} , x = 1,2,3, y= 1,2,3 일 때 $$
결합분포와 주변분포를 표로 나타내면,
| Y \ X | 1 | 2 | 3 | $f_Y$ |
| 1 | 1/36 | 2/36 | 3/36 | 1/6 |
| 2 | 2/36 | 4/36 | 6/36 | 2/6 |
| 3 | 3/36 | 6/36 | 9/36 | 3/6 |
| $f_Y$ | 1/6 | 2/6 | 3/6 | 1 |
위 경우 모든 x,y에 대해 아래의 식이 성립함을 확인할 수 있습니다. 이 경우 X,Y는 독립입니다.
$$ f(x,y) = f_X(x) f_Y(y) $$
'통계학 이야기' 카테고리의 다른 글
| 41. 확률분포의 분류 (1) | 2023.10.23 |
|---|---|
| 40. 확률변수의 공분산과 상관계수 (1) | 2023.10.22 |
| 38. 확률변수의 분산과 표준편차 (1) | 2023.10.19 |
| 37. 확률변수의 기대값(Expected Value) (1) | 2023.10.18 |
| 36. 확률함수 - 확률질량함수 & 확률밀도함수 (1) | 2023.10.17 |




