38. 확률변수의 분산과 표준편차

Chapter 38. 확률변수의 분산과 표준편차

 

1. 확률변수의 분산

 

일변량 자료에 대한 수치적 기술통계에서 표본들이 얼마나 퍼져 있는지를 나타내는 대표적인 것이 분산과 표준편차입니다. 확률변수의 산포를 알아보기 위한 분산과 표준편차를 알아낼 수 있습니다.

확률변수의 분산을 표본분산을 구하는 식으로부터 유도해 올 수 있습니다.

 

(1) 표본분산

 

 분산은 관측값에서 중심위치(평균)를 뺀 값을 제곱하고 그것을 모두 더한 값입니다.

 표본공간은 확률실험에서 나왔고 나온 원소들을 숫자로 바꿔 주는 것이 확률변수입니다.

따라서 확률변수는 수치자료라 할 수 있습니다. 확률변수의 분산을 구할 때 일단 표본분산의 방법에서 시작합니다.

 

표본분산을 구하는 식은 아래와 같습니다.

 

표본크기를 n이라 할 때,

$$S^2 = \frac{1}{n-1} \sum_{i=1}^{n}(x_i - \bar{x})^2$$

 

앞서 기대값을 표본평균으로 부터 유도할 때, 각 표본의 비율을 $p_i =\frac{n_i}{n}$ 라 하고 식은 아래와 같이 표현했습니다.

 

$$\begin{align} \bar{x} = \sum_{i=1}^6 x_i p_i \end{align}$$

 

같은 방법으로 위 표본분산은 아래와 같이 표현할 수 있습니다.

 

$$S^2 = \frac{1}{n-1} \sum_{i=1}^{n}n_i(x_i - \bar{x})^2$$

이 식에 분자와 분모에 n을 각각 곱해주면,

 

$$S^2 = \frac{n}{n-1} \sum_{i=1}^{n}n_i(x_i - \bar{x})^2 \times \frac{1}{n}$$

 

$p_i =\frac{n_i}{n}$ 를 대입해주면,

 

$$S^2 = \frac{n}{n-1} \sum_{i=1}^{n}(x_i - \bar{x})^2 p_i$$

 

(2) 확률변수 분산의 일반식

 

앞서 기대값에서와 마찬가지로 표본크기 n 이 계속 커진다면, 표본은 모집단에 이르고, 표본분산은 모분산이 되고 결국 각 표본의 비율 $p_i$ 는 확률함수 $f(x_i)$ 가 됩니다.

그리고 $\frac{n}{n-1}$ 은 1이 됩니다. 이를 식으로 표현하면,

 

$$S^2 = \frac{n}{n-1} \sum_{i=1}^{n}(x_i - \bar{x})^2 p_i$$

$$\sigma^2 = \sum_{i=1}^{k}(x_i - \mu)^2f(x_i)$$

일반적으로 모분산을 $\sigma^2$ (시그마) 로 표시합니다.

 

이제 확률변수 X의 분산을 Var(X)라 표시하면

 

$$Var(X) = \sum_{x}(x - \mu)^2f(x)$$

 

이 분산식은 확률변수 X에 변환된 함수의 기대값으로 나타낼 수 있습니다.

$$E((X-\mu)^2)$$

 

위 분산식을 풀어 정리해보면,

 

$$Var(X) = \sum_{x}(x - \mu)^2f(x)$$

$$Var(X) = \sum_{x}(x^2 - 2x\mu+\mu^2)f(x)$$

$$Var(X) = \sum x^2f(x) -2\mu \sum xf(x)+ \mu^2\sum f(x)$$

 

이전 회차에서 기대값은 $\sum xf(x) = \mu , \sum f(x) = 1$ 이므로 이를 대입하면,

 

$$Var(X) = \sum x^2 f(x) - 2 \mu^2 + \mu^2 = \sum x^2 f(x) - \mu^2$$

 

이를 간략히 기대값으로 표현하면,

$$Var(X) = E(X^2) - E(X)^2$$

 

2. 확률변수의 표준편차

표준편차는 분산의 제곱근입니다.

 

$$\sigma = \sqrt{\sigma^2} =\sqrt{Var(X)} = SD(X)$$

 

3. 이산확률변수의 분산과 표준편차

◈ 예제 : 동전 3개 던지기

 

 이전회차에서 사용했던 동전을 3개 던지는 확률실험을 할 때 앞면의 수를 나타내는 확률변수 X는 아래와 같이 나타납니다.

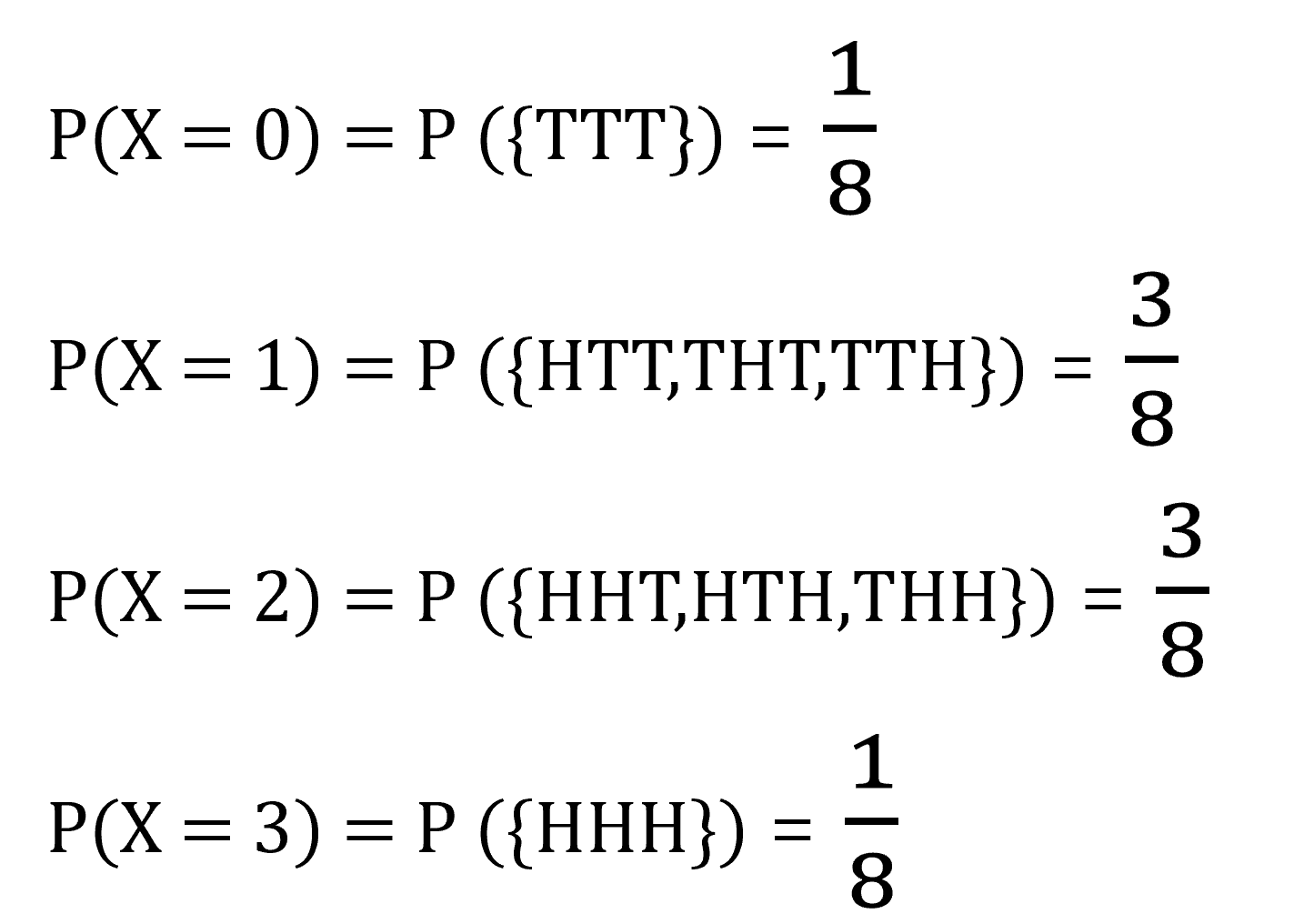
이를 확률질량함수로 표현하면, 아래와 같이 나타냈습니다.

$$f(0) = \frac{1}{8} , f(1) = \frac{3}{8} , f(2) = \frac{3}{8} , f(3) = \frac{1}{8}$$

 

기대값은 

$$\begin{align} E(X) =  \sum_{x=0}^{3} xf(x) \end{align} = 1.5$$

 

제곱한 값의 기대값은

$$\begin{align} E(X^2) =  \sum_{x=0}^{3} x^2f(x) \end{align} = 3$$

 

이제 분산 Var(X)를 구하면,

 

$$Var(X) = E(X^2) - E(X)^2 = 3 - 1.5^2 = 0.75$$

 

표준편차 SD(X) 는,

 

$$SD(X) = \sqrt{Var(X)} = \sqrt{0.75} = 0.866$$

 

4. 연속확률변수의 분산과 표준편차

연속확률변수 X의 기대값은,

 

$$E(X) = \int xf(x)dx$$

 

확률변수 X의 분산을 구하는 식은,

$$Var(X) = E(X^2) - E(X)^2$$

 

여기에 연속확률변수의 기대값을 대입하여 적용하면, $$Var(X) = \int (x - \mu)^2 dx = \int x^2f(x) dx - ( \int xf(x)dx)^2$$

 

◈ 예제 : 0~12까지의 숫자가 표시된 돌림판

 

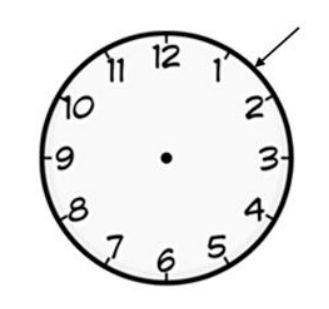
왼쪽 그림과 같이 숫자가 표시된 돌림판을 돌려서 바늘이 위치하는 사건을 확률변수 X라 할 때,

 

확률밀도함수는 $f(x) = \frac{1}{12} , 0 < x \leq 12$ 입니다.

 

 

 

 

 

확률변수 X의 기대값은,

$$E(X) = \int_{0}^{12} x \frac{1}{12} dx = \frac{1}{12} \int _{0}^{12} x dx = \frac{1}{12} \frac{12^2}{2} = 6$$

 

$X^2$ 의 기대값은,

$$E(X^2) = \int_{0}^{12} x^2 \frac{1}{12} dx = \frac{1}{12} \int _{0}^{12} x dx = \frac{1}{12} \frac{12^3}{3} = 48$$

 

따라서 분산 Var(X),

$$Var(X) = E(X^2) - E(X)^2$$

$$Var(X) = 48 - 6^2 = 12$$

 

표준편차 SD(X) 는,

$$SD(X) = \sqrt{Var(X)} = \sqrt{12} = 3.464$$

 

5. 분산의 성질

확률변수 X의 분산을 알고 있을 때, aX+b의 분산은 얼마일까요?

 

결론부터 말하자면,

$$Var(aX+b) = a^2 Var(X)$$

로 나타납니다.

이렇게 나타나는 이유는, 위치의 변화를 주는 상수 b는 영향을 주지 않고, 분산은 측정단위의 제곱이기 때문에 상수 a는 제곱하여 곱합니다.

 

기대값의 성질을 이용하여 유도해 보겠습니다.

 

$$E(aX+b) = aE(X)+b = a\mu + b$$

 

$$Var(X) = \sum_{x}(x - \mu)^2f(x)$$

 

위 두 식을 이용하여 Var(aX+b) 를 구해보겠습니다.

 

$$Var(aX+b) = \sum (ax+b - (a\mu+b))^2 f(x)$$

$$Var(aX+b) = \sum (ax-a\mu)^2 f(x) = \sum(a(x-\mu))^2 f(x)$$

여기서 $a^2$은 상수이므로 앞으로 빼주면,

$$Var(aX+b) = a^2 \sum (x-\mu)^2 f(x) = a^2Var(X)$$

 

표준편차 SD(aX+b) 는 ,

 

$$SD(aX+b) = \sqrt{Var(aX+b)} = \sqrt{a^2Var(X)} = |a| SD(X)$$

 

표준편차에서 음수는 없기 때문에 절대값으로 표기해야 합니다.