37. 확률변수의 기대값(Expected Value)

Chapter 37. 확률변수의 기대값(Expected Value)

 

확률변수의 통계량은 확률분포를 표현하기 위한 값들이며, 이 값들은 확률함수를 통해 계산할 수 있습니다.

 

1. 기대값(Expected Value)

 

확률변수의 기대값은 해당 확률변수가 가질 수 있는 각 값에 대해 그 값들의 가중 평균을 계산한 것이라 말할 수 있습니다. 기대값은 확률변수의 "평균적인" 값으로 생각할 수 있습니다.

 

확률변수에 대해 평균적으로 기대하는 값 = 모평균(population mean) = 확률분포(또는 모집단)의 무게중심

 

하나의 확률과정에 의해 결정되는 숫자는 하나의 값 주위로 분포합니다.

이 때 기대값(Expected Value)은 분포의 무게중심에 해당되는 값입니다. 즉 확률변수의 기대값은 확률분포의 중심위치를 말합니다.

 

(1) 표본평균에서 기대값 유도

 

확률변수 각 값은 각각의 자료라고 할 수 있습니다. 확률변수의 기대값은 표본평균을 구하는 방식에서 유도해올 수 있습니다.

 

우선, 표본평균의 일반식은 아래와 같습니다.

 

$$ \begin{align} \bar{x} =\frac{ x_1+x_2+\dots+x_n}{n} = \frac{1}{n} \sum_{i=1}^n x_i \end{align}$$

 

◈ 예제 : { 1, 2, 3, 4, 5, 6}으로 이루어진 모집단으로부터 5개의 표본을 무작위로 선택해서 얻은 값이 1,1,2,5,6 이라 할 때,

 

 표본평균을 계산하면, 아래와 같이 할 수 있습니다.

 

 $$ \begin{align} \bar{x} =\frac{ 1+1+2+5+6}{5} = 3  \end{align}$$

 

 위 계산산식을 각 관측된 값에 그 값이 차지하는 비율을 곱하여 더한 것으로 표시할수 있습니다.

 

$$ \begin{align} \bar{x} = 1 \times \frac{2}{5} + 2 \times \frac{1}{5} + 3 \times \frac{0}{5} + 4 \times \frac{0}{5} + 5 \times \frac{1}{5} + 6 \times \frac{1}{5} = 3  \end{align}$$

 

이를 일반식으로 표현하면,

 표본크기 : $ n, x_i = i$ 라 했을 때, $ n_i $ 값이 i 표본의 수

$$ \begin{align} \bar{x} = x_1 \times \frac{n_1}{n} + x_2 \times \frac{n_2}{n} + x_3 \times \frac{n_3}{n} + x_4 \times \frac{n_4}{n} + x_5 \times \frac{n_5}{n} + x_6 \times \frac{n_6}{n} \end{align}$$

간략히는

$$ \begin{align} \bar{x} = \sum_{i=1}^6 x_i \frac{n_i}{n} \end{align}$$

 

여기서 각 표본의 비율을 p라 한다면, $ p_i =\frac{n_i}{n} $ 라 할 수 있습니다.

따라서, 위 식은 아래와 같이 표현할 수 있습니다.

 

$$ \begin{align} \bar{x} = \sum_{i=1}^6 x_i p_i \end{align}$$

 

(2) 기대값의 일반식

 

표본크기 n 이 계속 커진다면, 표본은 모집단에 이르고, 표본평균은 모평균이 되고 결국 각 표본의 비율 $p_i$ 는 확률함수 $ f(x_i) 가 됩니다. 이를 식으로 표현하면,

 

$$ \begin{align} \bar{x} = \sum_{i=1} x_i p_i = \sum_{i=1} x_i f(x_i)= E(X)= \mu \end{align}$$

 

기대값은 E(X) 혹은 $\mu$(뮤)로 표기합니다.

 

기대값을 구하는 방법은 이산확률변수인지 연속확률변수인지에 따라 다르게 계산합니다.

이산확률변수는 확률질량함수를 연속확률변수는 확률밀도함수를 각각 사용하여 계산합니다.

각각의 계산식은 아래와 같습니다.

 

▶ 이산확률변수 X 의 기대값

$$ \begin{align} E(X) =  \sum_{x} xf(x_i) = \mu \end{align}$$

 

▶ 연속확률변수 X 의 기대값

 $$ \begin{align} E(X)= \int_{x} xf(x)dx = \mu \end{align}$$ 

 

2. 확률변수의 변환(Transfromation)

 

확률변수의 변환이란 어떤 함수를 통해서 또 다른 확률함수를 만드는 것입니다. 이미 만들어진 확률변수 그 자체보다는 변환을 해서 사용해야하는 경우가 있습니다.

변환된 확률변수도 여전히 확률변수이기 때문에 기존의 확률변수의 성질을 그대로 가지고 있습니다.

또한 변환된 확률변수의 확률분포도 존재하게 됩니다.

 

◈ 예제 : 확률변수 X의 변환

 

 확률변수 X가 아래와 같은 확률분포를 가지고 있을 때,

 

x	-1	0	1	2
P(X=x)	0.1	0.3	0.2	0.4

  확률변수 X에 제곱을 하여 변환한 확률변수를 W 라고 했을 때, 

$$ W = X^2 $$

로 나타낼 수 있습니다. 이 때 W의 확률분포를 구하려면, 기존의 확률변수 값과 연결하면 됩니다.

x	-1	0	1	2
P(X=x)	0.1	0.3	0.2	0.4
w	1	0	1	4

 P(W=0) = 0.3 , P(W=1) = 0.1+0.2 = 0.3 , P(W=4) = 0.4

 

변환된 확률함수 W의 기대값을 구하면,

$$ E(W) = 0 \times 0.3 + 1 \times 0.3 + 4 \times 0.4 = 1.9 $$

 

이 식을 X의 관점에서는 아래와 같이 표현할 수 있습니다.

$$ E(X^2) = 0^2 \times 0.3 + (-1^2 \times 0.1 + 1^2 \times 0.2)+ 2^2 \times 0.4 = 1.9 $$

 

이것을 일반식으로 표현하면,

$$ E(W) = \sum_{x=-1}^{2} x^2f = E(X^2) $$

 

즉, 변환전 x의 값인 -1,0,1,2 를 넣으면 변형된 제곱의 값인 0,1,4 의 확률에 대한 기대값으로 나오는 것입니다.

 

확률변수 X 변환함수를 Y 라 하면, Y = g(X) 로 표현할 수 있습니다.

이 변환된 함수 Y의 기대값은 아래와 같습니다.

 

▶ 이산확률변수 X 의 변환된 함수 Y 기대값

$$ E(Y) = E(g(X)) = \sum_{x} g(x) f_X(x) $$

 

▶ 연속확률변수 X 의 변환된 함수 Y 기대값

$$ E(Y) = E(g(X)) = \int_{x} g(x)f_X(x) $$

 

3. 기대값의 성질

 

확률변수의 기대값은 확률변수가 가질 수 있는 값들의 평균적인 값으로, 확률분포의 중심을 나타냅니다.

 

확률변수의 기대값에 대한 주요 성질은 다음과 같습니다.

 

 (1) 상수의 기대값은 상수 자체이다.

 

 임의의 상수 a의 기대값은 아래와 같이 구할 수 있습니다. 

 $$ E(a) = \sum_{x} af(x) $$

이 때 상수 a는 x에 영향을 받지 않으므로 앞으로 빼낼 수 있습니다.

$$ E(a) = a\sum_{x} f(x) $$

이전 회차에서 $ \sum_{x} f(x) =1 $ 임을 알고 있습니다. 따라서 이를 적용하면,

$$ E(a) = a$$

 

상수의 기대값은 상수 자체임을 알 수 있습니다.

 

(2) 선형성

 

 확률변수에 대한 선형변환(상수배 및 상수덧셈)을 적용한 확률변수의 기대값은 해당변환을 각각 적용한 기대값의 선형조합과 동일합니다.

 

 확률변수 X를 aX+b로 변환했을 때의 기대값은 아래와 같이 구할 수 있습니다. (a,b는 상수)

$$ E(aX+b) = \sum (ax+b)f(x) $$

이를 각각 배분하여 표현하면,

$$ E(aX+b) = \sum axf(x) + \sum bf(x) = a\sum xf(x)+b $$

상수 a를 앞으로 빼고, $\sum bf(x)=b$임은 상수의 기대값에서 확인하였습니다.

$\sum xf(x) = E(X)$ 는 X의 기대값입니다. 따라서, 이를 간략히 정리하면, 아래와 같습니다.

$$ E(aX+b) = aE(X) + b $$

 

결국 확률변수에 대한 선형변환은 각각 적용한 기대값의 선형조합과 동일합니다.

 

(3) 변환된 확률변수 합의 기대값

 확률변수 X의 변환된 함수를 $ g_1(X), g_2(X) $ 라 할 때 두 함수 합의 기대값은 아래와 같습니다.

 

$$ E(g_1(X)+g_2(X)) = \sum_{x} (g_1(x)+g_2(x))f(x) $$

이를 각각 배분하여 표현하면,

$$ E(g_1(X)+g_2(X))= \sum g_1(x)f(x) + \sum g_2(x)f(x) = E( g_1(X))+ E( g_2(X)) $$

 

변환된 두 함수의 합의 기대값은 각각의 함수의 기대값의 합과 같습니다.

 

◈ 예제 : 동전 3개 던지기

 

 이전회차에서 사용했던 동전을 3개 던지는 확률실험을 할 때 앞면의 수를 나타내는 확률변수 X는 아래와 같이 나타납니다.

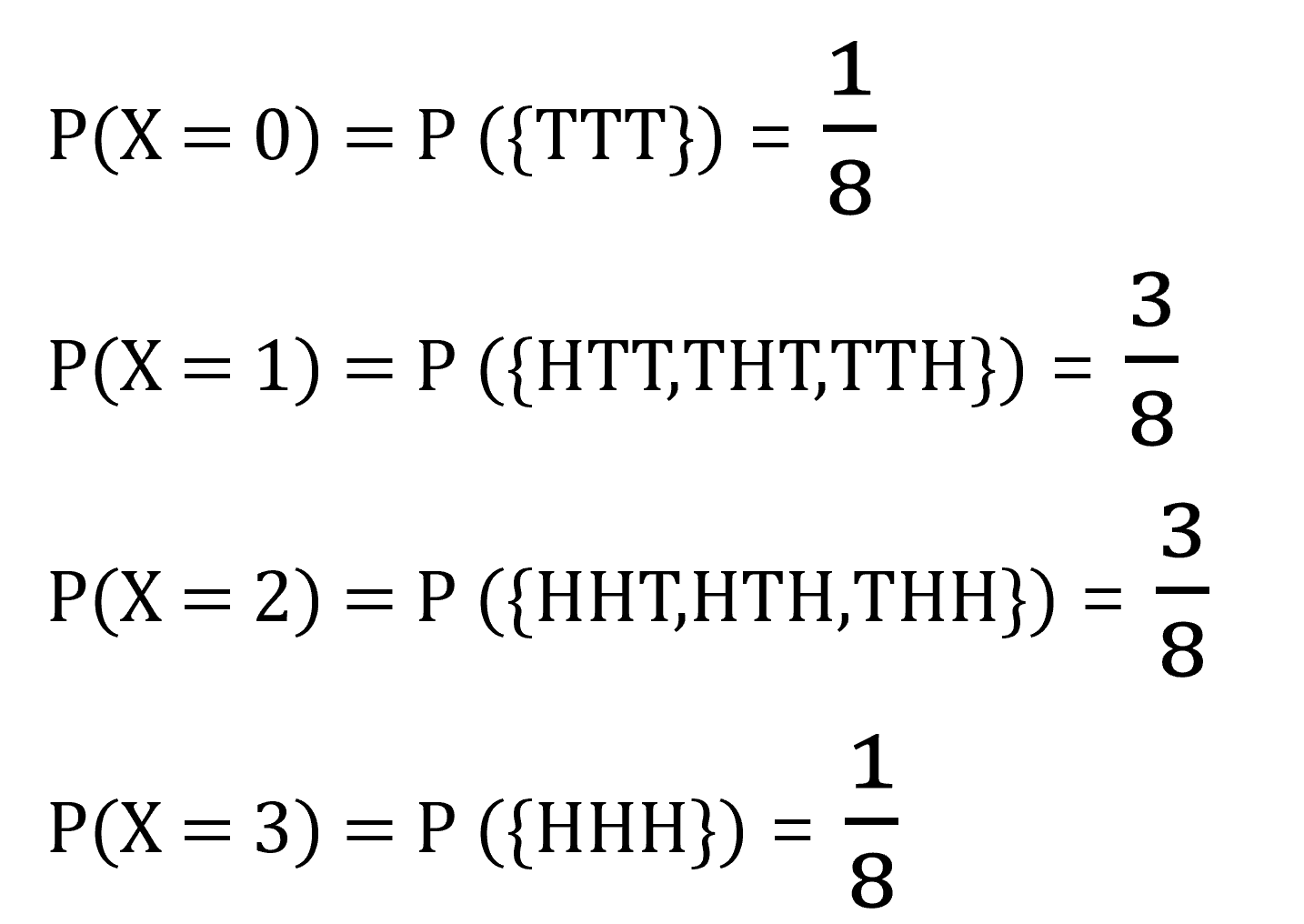
이를 확률질량함수로 표현하면, 아래와 같이 나타냈습니다.

$$ f(0) = \frac{1}{8} , f(1) = \frac{3}{8} , f(2) = \frac{3}{8} , f(3) = \frac{1}{8} $$

 

 

(1) 확률변수 X에 대한 기대값은 ?

 

$$ \begin{align} E(X) =  \sum_{x=0}^{3} xf(x) \end{align}$$

$$ = 0 \times \frac{1}{8} + 1 \times \frac{3}{8} + 2 \times \frac{3}{8}+ 3 \times \frac{1}{8} = \frac{12}{8} = 1.5 $$

 

(2) 확률변수 X에 제곱한 값의 기대값은 ?

 

$$ \begin{align} E(X^2) =  \sum_{x=0}^{3} x^2f(x) \end{align}$$

 

$$ = 0^2 \times \frac{1}{8} + 1^2 \times \frac{3}{8} + 2^2 \times \frac{3}{8}+ 3^ \times \frac{1}{8} = 3 $$

 

(3) 확률변수 X를 변환한 함수 $(X-1.5)^2$ 의 기대값은 ?

 

$$ \begin{align} E((X-1.5)^2) =  \sum_{x=0}^{3} (x-1.5)^2f_X(x) \end{align}$$

 

위 식을 펼쳐보면,

 

$$ = \sum_{x=0}^{3} x^2f_X(x) -3 \sum_{x=0}^{3} f_X(x) + \sum_{x=0}^{3} 1.5^2f_X(x) $$

 

각 항은 아래와 같이 나타낼 수 있습니다.

$$ = E(X^2) - 3E(X) +1.5^2 = 0.75 $$

 

 

확률변수의 기대값은 확률분포의 특성을 나타내는 중요한 지표로서, 확률변수의 특성과 분포를 이해하는데 도움을 줍니다.