| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- html
- version 2
- 산점도
- 인공지능
- 반복있음
- 에세이
- 정규분포
- 반복없음
- 혼합효과모형
- 경제학
- 글쓰기
- JavaScript
- 변량효과모형
- 분산분석
- 해운업
- 통계학
- 티스토리챌린지
- 확률
- css
- 이원배치 분산분석
- 고정효과모형
- 데이터 과학
- r
- 변동분해
- version 1
- 이항분포
- 가설검정
- 추정
- 회귀분석
- 오블완
- Today
- Total
생각 작업실 The atelier of thinking
63. 가설 검정(Hypothesis Testing) 본문
Chapter 63. 가설 검정(Hypothesis Testing)
통계적 추론은 추론 목적에 따라 크게 추정과 가설검정으로 나눌 수 있습니다.

가설검정은 주어진 가설에 대해 데이터를 사용하여 통계적으로 검증하는 것을 의미합니다.
1. 가설의 개념과 종류
(1) 가설 검정(Hypothesis Testing)의 개념
가설 검정은 모집단의 모수 또는 분포에 대한 추측이나 주장을 설정하고 이것의 옳고 그름을 표본의 정보를 이용하여 확률적으로 판정하는 과정을 말합니다.
가설 검정은 모집단에 대한 가설을 세우고, 이를 테이터로부터 검증하는 방법입니다.
가설 검정은 귀무가설과 대립가설을 설정하고, 귀무가설이 기각되면 대립가설을 채택합니다.
(2) 가설(Hypothesis)의 종류
가설이란 모수 또는 분포(모집단)에 대한 추측이나 주장을 말합니다. 가설은 귀무가설과 대립가설로 나눌 수 있습니다.
▶ 귀무가설(Null Hypothesis)
검증하고자 하는 가설로, 보통은 모집단에 대한 기존의 믿음이나 주장을 담고 있습니다.
▶ 대립가설(Alternative Hypothesis)
귀무가설을 기각하게 되면 채택할 가설입니다. 대립가설은 귀무가설과 모순되는 내용을 담고 있습니다.
※ 검정이란 무엇의 내용이 바르고 틀린지를 살펴보고 결정하는 일입니다.
◈ 예제 : 기존 파이의 평균 칼로리는 165kcal 이었습니다.
가설검정을 통해 새로운 파이는 기존의 파이보다 칼로리가 낮다는 것을 보이고자 합니다.
이 경우 귀무가설과 대립가설을 각각 설정한다면 ?
귀무가설은 기존의 믿음이나 주장을 담고 있습니다. 따라서 H0≥165로 나타낼 수 있습니다.
대립가설은 귀무가설을 기각되면 채택할 가설입니다. 따라서 H1<165 로 나타낼 수 있습니다.
(3) 귀무가설과 대립가설의 기본형태
모수를 ϕ 로, 기존의 값을 ϕ0 로 표시하였을 때,
| 상황 | 귀무가설 (H0) | 대립가설 (H1) |
| A | ϕ≤ϕ0 | ϕ>ϕ0 |
| B | ϕ≥ϕ0 | ϕ<ϕ0 |
| C | ϕ=ϕ0 | ϕ≠ϕ0 |
상황 A,B 는 단측검정(one-sided test) , 상황 C는 양측검정(two-sided test) 입니다.
가설검정에서 중요한 것은 첫 출발점인 가설을 잘 설정하는 것입니다. 보이고자 하는 가설을 대립가설로, 기존의 상황을 귀무가설로 설정합니다.
2. 가설 검정의 원리
(1) 명제의 역, 이, 대우
가설 검정의 원리를 이해하기 위해서는 먼저 명제의 역,이, 대우에 대하여 알아볼 필요가 있습니다.
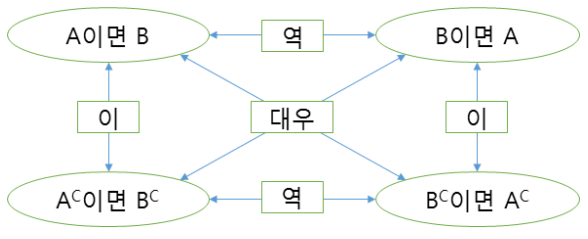
특히 알아야 할 것은, "A 이면 B 가 참(거짓)이면 그 대우도 항상 참(거짓)" 이라는 것입니다.
이것은 방법적으로 원래의 명제를 증명하기 어렵다면, 대우을 이용하여 증명하는 것입니다.
귀류법은 '잘못된 것을 뒤집어서 생각해보자'라는 의미로, 논리학에서 사용되는 증명 방법 중 하나입니다. 귀류법은 증명하고자 하는 명제를 부정하고, 그 부정 명제가 모순을 발생시킨다는 것을 보여서, 원래의 명제가 참임을 보이는 방법입니다.
예를 들어, "모든 A는 B이다."라는 명제가 있을 때, 이를 부정하면 "어떤 A는 B가 아니다."라는 명제가 되고 이 부정 명제가 모순을 발생시킨다면,"모든 A는 B이다."는 참인 명제임을 증명할 수 있습니다.
귀류법은 수학적 증명이나 철학적 논의에서 많이 사용되는 방법 중 하나입니다.
(2) 가설 검정의 증명 방법
가설검정의 목적은 대립가설이 참 임을 보이고자 하는 것 입니다.
즉, "정상적인 표본에서 대립가설은 참이다." 라는 명제를 증명하는 것입니다. 그러나, 정상적인 표본안에서 대립가설이 참 임을 밝히는 것은 어렵기 때문에 그 대우인 "귀무가설이 참이면 비정상적인 표본이다."라는 것을 증명하는 방법을 사용하게 됩니다.
여기서 표본이 정상인지 비정상인지를 무엇을 보고 판단할 것인가에 대한 답은 검정통계량(Test Statistics)이고, 어느 정도되어야 비정상이라고 할 수 있는가에 대한 답은 유의수준(Significant Level)이라 할 수 있습니다.
가설검정의 기본 원리는 귀무가설하에서 표본의 비정상성 여부를 통해 대립가설의 타당성을 확인하는 것입니다. 이 때 기준으로 사용되는 것이 검정통계량과 유의수준입니다.
3. 검정통계량과 오류
(1) 검정통계량(Test Statistic)
귀무가설 하에서 표본의 비정상성을 결정하기 위해 사용되는 통계량
통계량은 미지의 모수를 포함하지 않은 확률변수이면 확률분포가 존재합니다.
통계값이 발생가능성이 희박한 위치에 있는 경우 귀무가설 기각(reject), 그렇지 안은 경우에는 유지(retain) 또는 채택(accept) 합니다.
검정통계량을 유도하는 방법에는 Most Powerful Test(최강검정력), Likelihood Ratio Test(가능도비 검정, LRT), Score Test 등 (수리통계학 범위) 등이 있습니다. 주로 점추정량을 기반으로 유도합니다.
귀무가설하에서 검정 통계량의 확률분포를 이용하여 표본의 정상/비정상을 판정합니다.
기각역(rejection region) : 비정상영역 귀무가설 기각(reject)
채택역(acceptance region) : 정상영역 귀무가설 유지(retain/accept)
◈ 예제 : 기존 파이의 평균 칼로리는 165kcal 이었습니다.
가설검정을 통해 새로운 파이는 기존의 파이보다 칼로리가 낮다는 것을 보이고자 합니다.
이 때의 귀무가설과 대립가설은 H0≥165 와 H1<165 였습니다.
여기서 사용할 수 있는 검정통계량은 표본평균(ˉX)입니다. 예를 들어,귀무가설을 기준으로 검정통계량인 표본평균은 작으면 작을수록 비정상적 자료가 되어 귀무가설은 기각됩니다. 이 때 정상/비정상의 기준은 유의수준(significance level)으로 결정하게 됩니다.
(2) 오류의 종류
가설 검정을 하다보면 오류가 발생하게 됩니다. 오류는 크게 2 종류로 나눌 수 있습니다.
귀무가설이 참임에도 대립가설을 채택하는 경우와 대립가설이 참임에도 귀무가설을 채택하는 경우입니다.
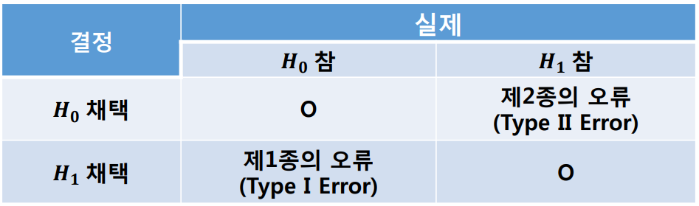
▶ 제 1 종의 오류(Type I Error)
귀무가설이 참임에도 대립가설을 채택하는 경우를 제1종의 오류라고 부릅니다. 이 제1종의 오류를 확률로 표시한 것이 유의수준(significance level)입니다. 이 오류의 확률은 낮을수록 좋습니다.
▶ 제 2 종의 오류(Type II Error)
대립가설이 참임에도 귀무가설을 채택하는 경우를 제2종의 오류라고 부릅니다. 1에서 이 제2종의 오류 확률을 뺀 것을 검정력(statistical power)이라고 합니다.
4. 유의 수준과 검정력
(1) 유의 수준(Significance Level)
통계적인 가설검정에서 사용되는 기준값입니다.
가설검정에서 귀무가설이 맞는데도 불구하고 기각하는 오류를 범할 확률을 미리 정한 값입니다.
일반적으로 유의수준은 α로 표시하고 95%의 신뢰도를 기준으로 한다고 했을 때, (1-0.95) 인 0.05는 유의수준 값이 됩니다.
유의수준 5%란 의미는 표본을 추출해서 나온 검정 통계량이 우연히 나타날 확률이 5%미만이라는 것입니다.
유의수준은 제1종의 오류 확률의 최대값으로 사용합니다.
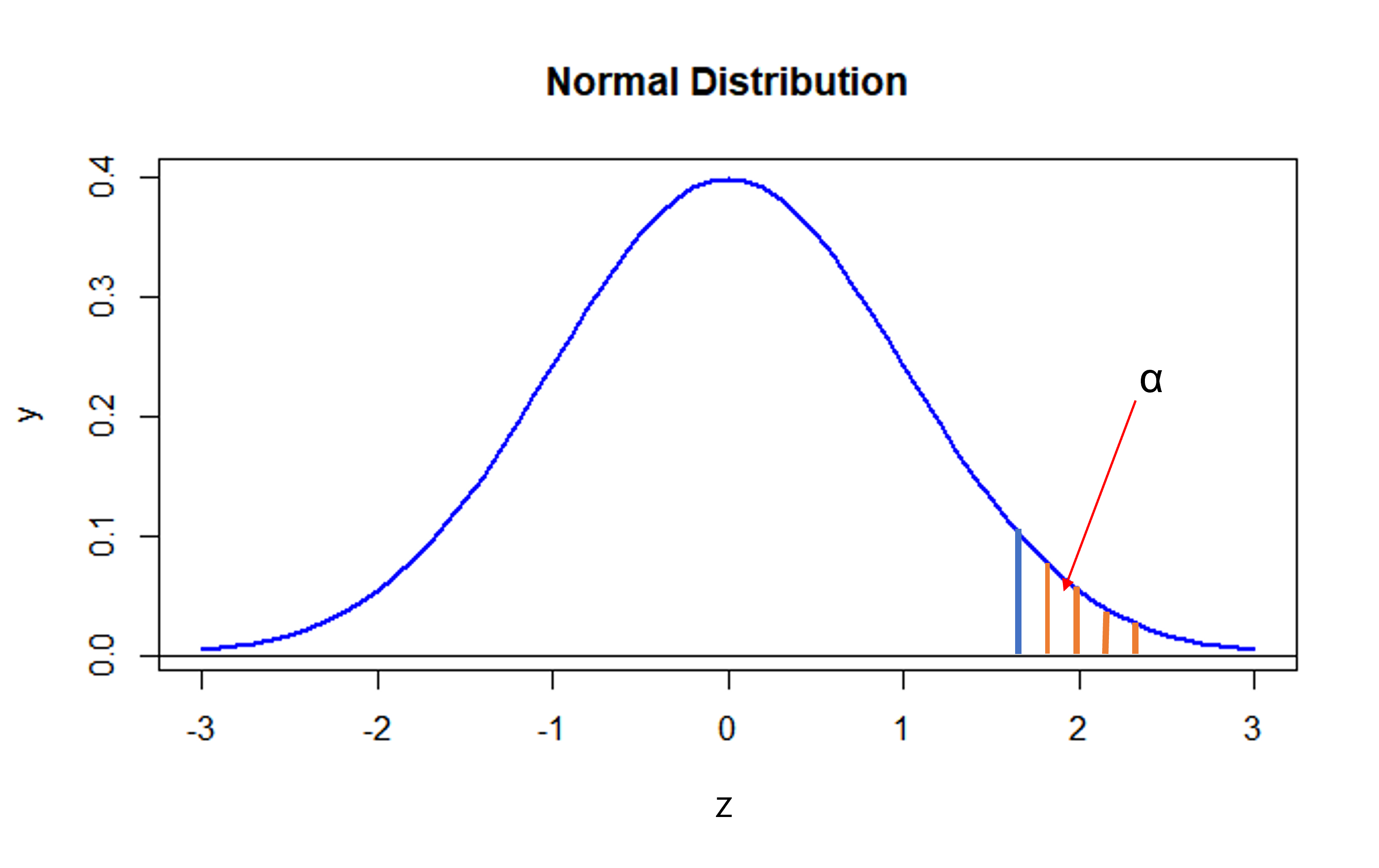
유의수준 α 를 결정할 때의 유의사항은, 귀무가설의 오류 확률이 낮을 수록 귀무가설이 아닌 대립가설을 선택할 확률이 줄어들게 됩니다. 이는 결과값에 대한 신뢰도가 높아진다고 할 수 있습니다.
따라서 α 의 값을 작게 설정하는 것이 좋습니다. 통상 α 값은 0.05,0.01,0.1 수준에서 결정되는 경우가 많습니다.
유의수준에 따라 검정원칙, 즉 기각역을 구할 수 있습니다.
◈ 예제 : 기존 파이의 평균 칼로리는 165kcal 이었습니다.
가설검정을 통해 새로운 파이는 기존의 파이보다 칼로리가 낮다는 것을 보이고자 합니다.
25개의 표본을 추출하고 분산은 202 입니다.
이 때 관측값 평균이 156kcal이었다면, 5% 유의수준에서 새로운 파이는 기존의 파이보다 칼로리가 낮다고 할 수 있을까?
귀무가설은 파이의 칼로리는 165kcal보다 크거나 같다라고 할 수 있습니다. 이를 식으로 표현하면,
H0≥165vsH1<165
이 때 n=25 이고 귀무가설하에서 검정통계량은 아래와 같습니다.
Z0=ˉX−μ20/√25∼N(0,1)
유의수준 α=0.05 로 설정할 때 기각역은 Z<−1.645 입니다.
관측값 평균이 156kcal 이므로 이를 ˉX에 대입하여 계산하면,
Z0=156−16520/√25=−2.25
−2.25<−1.645(유의수준α=0.05일때기각역)
즉, 검정통계량 -2.25 는 기각역에 있으므로 귀무가설을 기각합니다. 따라서, 5% 유의수준에서 새로운 파이의 평균 칼로리는 기존 파이의 칼로리보다 낮다고 할 수 있습니다.
(2) 검정력(Statistical Power)
검정력이란 대립가설이 참일 때, 이를 참으로서 결정할 확률이며, 귀무가설이 거짓일 때 이를 옳게 기각할 확률입니다. 이는 1에서 제2종의 오류 확률을 뺀 값으로 구합니다.( 1 - P(제 2종의 오류) )
검정력(Power) = 1- β 로 나타냅니다.
검정력이 높을수록 귀무가설이 거짓임에도 불구하고 옳게 기각할 가능성이 높아지므로, 좋은 가설검정을 위해서는 높은 검정력이 필요합니다.
다만, 기각역의 조정만으로 동시에 유의수준을 줄이고 검정력을 높일 수 없습니다.
가설검정에서 원하는 α와 β에 해당하는 표본크기를 조정하여 가능합니다.
5. 유의확률(P-Value)
유의확률은 검정통계량이 귀무가설을 지지하는 정도를 나타내는 확률값입니다.
표본 데이터에서 계산된 검정 통계량이 귀무가설을 지지하는 정도를 나타내는 값으로, 작을수록 귀무가설이 기각되기 쉽습니다.
◈ 예제 : 기존 파이의 평균 칼로리는 165kcal 이었습니다.
Z0=156−16520/√25=−2.25
이 때의 유의확률은,
P(Z<−2.25)=0.0122
앞서 유의수준 5%일 때 유의확률은 1.22% 이므로 귀무가설을 기각하게 됩니다.
그러나, 유의수준을 1%로 바꿔 결정한다면 유의확률 1.22%는 채택역에 속하게 되므로 귀무가설을 유지하게 됩니다. 유의확률을 알게 되면, 유의수준이 바뀌어도 검정통계량을 다시 구하지 않고도 결론에 이를 수 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 65. 모평균에 대한 통계적 추론 II (0) | 2024.02.18 |
|---|---|
| 64. 모평균에 대한 통계적 추론 I (1) | 2024.01.16 |
| 62. 추정(Estimation) - 구간 추정(Interval Estimation) (1) | 2023.12.28 |
| 61. 추정(Estimation) - 점 추정(Point Estimation) (0) | 2023.12.25 |
| 60. 통계적 추론(추론 통계학)의 개요 (2) | 2023.12.22 |




