| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 글쓰기
- 이항분포
- 변량효과모형
- version 1
- css
- 정규분포
- 고정효과모형
- 산점도
- 회귀분석
- 반복없음
- JavaScript
- 변동분해
- 티스토리챌린지
- 확률
- 반복있음
- html
- 두 평균의 비교
- 경제학
- 이원배치 분산분석
- 통계학
- 인공지능
- 에세이
- 모평균에 대한 통계적추론
- 가설검정
- 추정
- 혼합효과모형
- 분산분석
- 데이터 과학
- 오블완
- r
- Today
- Total
생각 작업실 The atelier of thinking
61. 추정(Estimation) - 점 추정(Point Estimation) 본문
Chapter 61. 추정(Estimation) - 점 추정(Point Estimation)
통계적 추론은 추론 목적에 따라 크게 추정과 가설검정으로 나눌 수 있습니다.
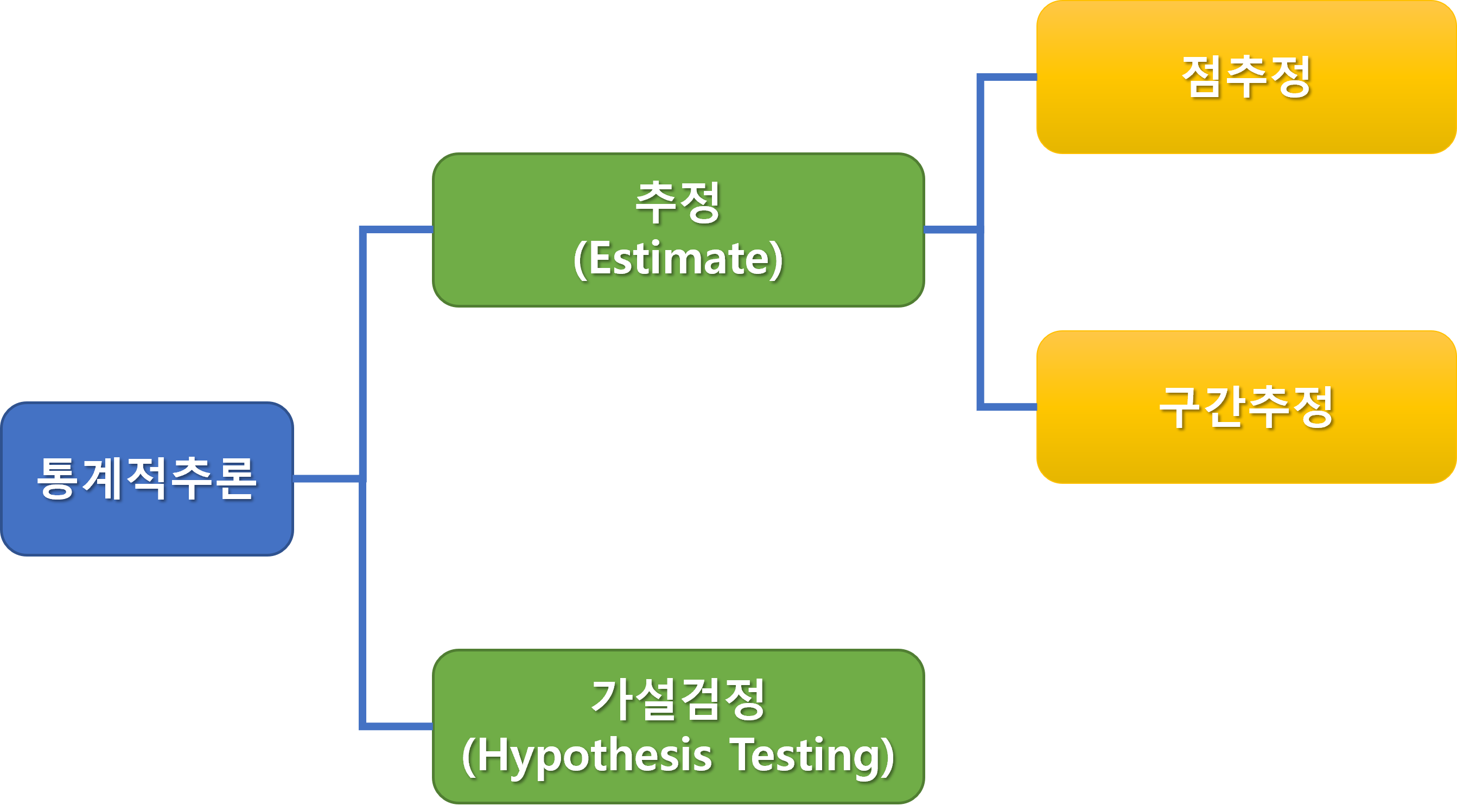
추정은 표본을 통해 모집단의 모수를 추측하는 것을 의미합니다.
추정은 표본의 정보를 활용하여 모집단에 대한 정보를 얻는 데에 중요한 역할을 합니다.
추정은 점추정과 구간추정으로 나눌 수 있습니다.
점추정은 하나의 값으로 모수를 추정하는 것을 의미하며, 대표적으로 표본평균이나 표본분산 등이 있습니다.
1. 점 추정
점 추정이란 미지의 모수를 표본의 어떤 함수(통계량, statistic)를 이용하여 어떤 값으로 추정하는 과정입니다.
점 추정은 하나의 값으로 모수를 추정하는 것을 의미합니다.
점 추정량을 계산하는 방법에는 여러 가지가 있지만, 대표적인 방법으로 적률법, 최대가능도 추정법, 최소제곱법 등이 있습니다.
(1) 적률법 (Method of Moments)
적률법은 확률분포의 모수를 추정하는 데 사용되는 추정방법으로 표본의 적률(moment)과 이론적인 적률을 일치시키는 원리에 기반합니다. 적률은 확률분포의 특성을 나타내는 데, 적률법은 이 특성을 이용하여 모수를 추정합니다.
대부분 확률분포에서 모수는 기대값으로 표시합니다.
정규분포에서 확률표본을 추출한 경우 아래와 같이 표현합니다.
$$ X_1,X_2,...,X_n \overset{\mathrm{iid}}{\sim} N(\mu , \sigma^2) $$
이 때 모수인 평균($\mu$)과 분산($\sigma^2$)을 기대값으로 나타내면, $\mu = E(X), \sigma^2 = E(X^2) - E(X)^2 $ 로 표현할 수 있습니다.
위 표본의 기대값으로 아래와 같이 모집단의 평균과 분산을 추정할 수 있습니다.
$$ \bar{X} = \frac{1}{n}\sum X_i → E(X) $$
표본평균을 가지고 n이 계속 커지면 모평균이 됩니다.
$ E(X^2) $은 $\frac{1}{n} \sum X_i^2 $으로 추정할 수 있습니다.
따라서 모평균은 표본평균으로 모분산은 아래와 같이 추정할 수 있습니다.
$$ \hat{\mu} = \bar{X}, \hat{\sigma}^2 = \frac{1}{n} \sum X_i^2 - \bar{X}^2 = \frac{1}{n} \sum(X_i - \bar{X})^2 $$
(2) 최대가능도 추정법 (Maximum Likelihood Estimation, MLE)
최대가능도 추정법은 R.A.Fisher 라는 분이 제안한 방법입니다. 통계에서 가장 중요한 방법 중에 하나 입니다.
최대가능도 추정법은 관측되 데이터를 바탕으로 모집단 분포의 모수를 추정하는 방법입니다. 이 방법은 주어진 데이터에서 가능도 함수를 최대화하는 모수 값을 찾는 것입니다.
가능도 함수는 모수를 알고 있을 때 주어진 데이터가 나타날 확률을 나타냅니다.
이 방법은 대규모 표본에서 일반적으로 잘 작동하지만, 작은 표본에서는 부정확할 수 있습니다.
가능도(Likelihood, 우도) 함수란 확률분포의 모수가, 어떤 확률변수의 표집값과 일관되는 정도를 나타내는 값입니다. 구체적으로, 주어진 표집값에 대한 모수의 가능도는 이 모수를 따르는 분포가 주어진 관측값에 대하여 부여하는 확률입니다.
◈ 예제 : 이항분포에서의 가능도 함수
아래와 같은 이항분포에서 성공할 확률은 모르고 있을 때 8이 관측되었다면, 8 이라는 데이터를 얻을 가능성은?
$$ X \sim B( 10, \theta ) , \theta : 성공확률 $$
여기서 성공은 8이 나오는 것을 의미합니다.
확률질량함수는 이렇게 표현할 수 있습니다.
$$ f(x ; \theta) = \binom{10}{x} \theta^x(1-\theta)^{10-x} , x = 0,1,...,10, 0 < \theta <1 $$
여기서 실제 데이터를 수집하였더니 $x$가 8이라는 값이 나왔을 때 $\theta$는 모르고 있는 상태입니다.
따라서, $\theta$ 가 0.1 일 때 8이 나올 확률은 얼마인가? 0.2 일때, 이런 식으로 쭉해서 0.9일 때를 대입해서 계산해볼 수 있습니다.
$$ \theta = 0.1 일 때, f(8 ; 0.1) \approx 0.0000 $$
$$ \theta = 0.2 일 때, f(8 ; 0.2) = 0.0001 $$
...
$$ \theta = 0.8 일 때, f(8 ; 0.8) = 0.3020 $$
$$ \theta = 0.9 일 때, f(8 ; 0.9) = 0.1937 $$
여기서 확률질량함수의 산출값은 각각의 $\theta $에서 8이라는 자료를 얻을 가능성을 말합니다.
이를 그래프로 나타내면, 아래와 같습니다.
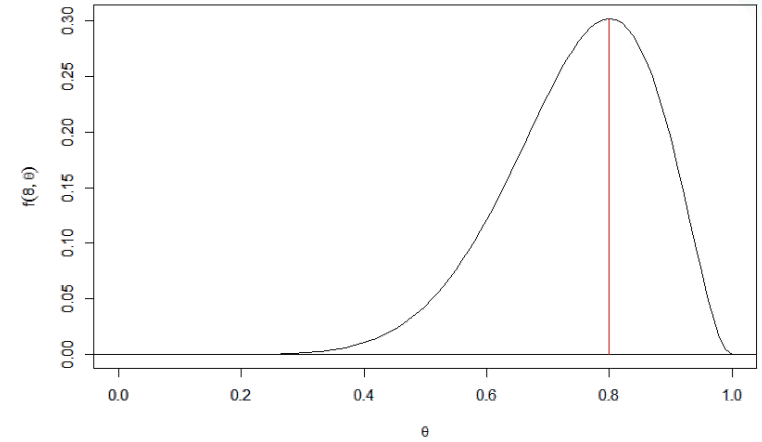
위 그래프에서 최대 높이의 위치가 최대 가능도 추정량( Maximum Likelihood Estimation, MLE) 입니다.
(3) 최소제곱법(Least Squares Estimation)
최소제곱법은 회귀분석에서 사용되는 방법으로, 표본의 관측값과 모델의 예측값 간의 잔차제곱합을 최소화하는 모수 값을 추정하는 방법입니다.
예를 들어, 선형회귀에서는 최소제곱법을 사용하여 최적의 회귀선을 찾아냅니다. 이 방법은 데이터의 분포에 대한 가정이 필요하고, 이상치에 민감할 수 있습니다.
2. 직관적인 점 추정량
점추정량은 위와 같은 방법을 통해서 구할 수 있습니다. 그러나 분포가 복잡하면 값을 구하기가 상당히 어렵습니다. 따라서, 이에 대한 대처방안으로 직관적인 추정량을 사용합니다.
| 모수 | ← | 통계량 |
| 모평균($\mu$) | ← | 표본평균($\bar{X}$) |
| 모비율($\theta$) | ← | 표본비율($P$) |
| 모분산($\sigma^2$) | ← | 표본분산($S^2$) |
| 모표준편차($\sigma$) | ← | 표본표준편차($S$) |
사실 점추정량이 정확히 모수와 일치할 가능성은 거의 없습니다.(대부분 연속확률변수이기 때문에) 그럼에도 불구하고 직관적인 추정량(통계량)을 사용하는 이유는 직관적으로 많이 사용하기 때문에 사용하기도 하지만, 사실은 이 값들은 앞에서 나왔던 많은 이론들을 통해서 이 값이 적절하다라고 이미 많은 사람들이 인정한 부분이기 때문에 그냥 사용해도 무방합니다.
추정량(estimator)은 확률변수이며 대문자로 표시하고, 추정치(estimate)는 실제 관측값이며 소문자로 표시합니다.
점추정량은 구간추정과 가설검정에서의 핵심적인 기준 통계량으로 사용되고 있습니다..
3. 좋은 추정량의 요건
점추정량이 좋은 추정량인지 아닌지 판정하는 기준이 있어야 합니다.
(1) 일치성(Consistency)
표본의 크기가 커질수록 추정량이 모수에 근사해야 합니다. 이를 일치성이 있다고 합니다. (대수의 법칙)
예를 들어, 표본의 평균이 모평균을 추정하는 추정량인 경우, 표본의 크기가 커질수록 표본평균은 모평균에 점점 더 가까워집니다. 이렇게 추정량이 모수에 근사해가는 것을 일치성이 있다고 합니다.
$$ X_1,X_2,...,X_n \overset{\mathrm{iid}}{\sim} N(\mu , \sigma^2) $$
$$ E(X_1) = \mu , \bar{X} → \mu$$
(2) 비편향성(Unbiasedness, 불편성)
추정량의 기대값이 모수와 같아야 합니다. 이를 비편향성이 있다고 합니다.
예를 들어, 표본의 평균이 모평균을 추정하는 추정량인 경우, 표본평균의 기대값은 모평균과 같습니다.
이렇게 추정량의 기대값이 모수와 같은 것을 비편향성이 있다고 합니다.
편향(편의)은 추정량의 기대값과 모수의 차이입니다.
$ \phi $ : 모수 , $\hat{\phi}$ : 추정량
$$ b(\hat{\phi}) = E(\hat{\phi}) - \phi $$
비편향 추정량은 기대값과 모수의 차이가 없을 때를 말합니다.
즉, $b(\hat{\phi})=0$ 일 때 비편향 추정량입니다.
평균의 기대값은 모수(모평균)와 같기 때문에 비편향입니다.
$$ E(\bar{X}) = \mu $$
표준편차는 편향(편의) 추정량(biased estimator)입니다.
$$ S^2 = \frac{1}{n-1} \sum(X_i-\bar{X})^2 → E(S^2) = \sigma^2 $$
$$E(S) \not= \sigma $$
$$ Var(S) = E(S^2) - E(S)^2 \ge 0 $$
$$ E(S^2) = \sigma^2 \ge E(S)^2 $$
$$ \sigma \ge E(S) $$
표준편차는 편향을 보이긴 하지만 편향의 정도가 미미하고, 위 일치성을 만족하여 크게 편향에 대한 영향이 없어 그대로 사용합니다.
(3) 효율성
추정량의 분산이 작을수록 좋습니다. 이를 효율성이 있다고 합니다.
예를 들어, 분산이 작은 추정량은 다른 추정량보다 표본의 크기가 크지 않은 경우에도 추정값이 더 가까이 모수에 있을 가능성이 큽니다. 이렇게 추정량의 분산이 작은 것을 효율성이 있다고 합니다.
추정량을 비교하는 측도로는 MSE(Mean Square Error)를 사용합니다.
$$ MSE(\hat{\phi}) = E((\hat{\phi}-\phi)^2) $$
$$ =E((\hat{\phi}-E(\hat{\phi})+E(\hat{\phi})-\phi)^2)$$
$$ = Var(\hat{\phi})+b(\hat{\phi})^2 $$
MSE는 분산과 bias 제곱의 합으로 표현되며, 작을수록 더 효율적입니다.
'통계학 이야기' 카테고리의 다른 글
| 63. 가설 검정(Hypothesis Testing) (0) | 2024.01.04 |
|---|---|
| 62. 추정(Estimation) - 구간 추정(Interval Estimation) (1) | 2023.12.28 |
| 60. 통계적 추론(추론 통계학)의 개요 (2) | 2023.12.22 |
| 59. 카이제곱분포(Chi-square Distribution) - 연속확률분포 (0) | 2023.12.20 |
| 58. T 분포(T - Distribution) - 연속확률분포 (0) | 2023.12.15 |





