| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 오블완
- 분산분석
- 이항분포
- JavaScript
- 변동분해
- 경제학
- 회귀분석
- 이원배치 분산분석
- version 1
- 반복없음
- 에세이
- 산점도
- 티스토리챌린지
- 가설검정
- 추정
- 확률
- 변량효과모형
- version 2
- 혼합효과모형
- 통계학
- 데이터 과학
- 인공지능
- 반복있음
- 고정효과모형
- r
- 글쓰기
- 정규분포
- 해운업
- html
- css
- Today
- Total
생각 작업실 The atelier of thinking
55. R 을 이용한 표집분포 & 몬테카를로 모의실험 본문
Chapter 55. R을 이용한 표집분포 & 몬테카를로 모의실험
1. 표집분포(Sampling Distribution)
표집분포는 모집단으로부터 표본을 추출했을 때, 어떤 통계량(예: 표본평균,표본분산)의 분포를 말합니다.
표집분포는 모집단으로부터 추출된 표본에서 계산된 통계량의 분포이기 때문에, 모집단에서 추출된 모든 표본에 대한 정보를 제공합니다. 이는 모집단의 모든 개체에 대한 정보를 얻기 어려운 경우에 표집분포를 사용하여 모집단을 추론하는 것이 더 효과적이기 때문입니다. 또한, 표집분포를 사용하면 모집단에 대한 가정이 필요없으며, 모집단의 분포가 무엇인지 알지 못해도 추론을 수행할 수 있습니다. 따라서, 통계적 추론에서는 표집분포를 사용하여 모집단의 특성을 추론하는 것이 일반적입니다.
◈ 예제 : 확률분포가 다음과 같을 때
| x | 0 | 1 | 2 |
| P(X=x) | 25 | 25 | 15 |
x <- c(0,1,2)
p <- c(2/5,2/5,1/5)
plot(x,p,type="h",lwd=3,col='blue',ylab = "P(X=x)",ylim = c(0,0.4))
abline(h=0)
두 개의 확률표본을 추출한 경우, 두 표본의 평균의 분포를 그래프로 그리면,
| ˉx | 0 | 12 | 1 | 32 | 2 |
| P(ˉX=ˉx) | 425 | 825 | 825 | 425 | 125 |
x_bar <- c(0,0.5,1,1.5,2)
p_bar <- c(4/25,8/25,8/25,4/25,1/25)
plot(x_bar,p_bar,type="h",lwd=3,col='blue',xlab=expression(bar(x)),ylab=expression(f(bar(x)))
)
abline(h=0)
2. 몬테카를로 모의실험(Monte Carlo Simulation)
몬테카를로 모의실험은 확률적인 상황에서의 다양한 변수들이 어떻게 작용하는지를 알아보기 위해 확률분포를 이용하여 가상의 실험을 반복적으로 수행하는 방법입니다. 이 방법은 실제로 실험을 수행하기 어려운 복잡한 문제들에 대한 근사적인 해법을 찾는 데 많이 사용됩니다.
몬테카를로 모의실험은 주어진 확률분포에서 무작위로 추출한 표본들을 이용하여 실제 실험에서 얻을 수 있는 데이터와 비슷한 결과를 만들어 냅니다. 이를 통해, 예를 들어 어떤 공정의 불량률을 추정하거나, 금융분야에서 옵션가격을 예측하는 등 다양한 분야에서 응용됩니다.
몬테카를로 모의실험에서는 난수 생성기를 사용하여 무작위로 추출한 표본들을 이용합니다. 따라서, 난수 생성기의 성능이 모의실험 결과에 영향을 미칩니다. 따라서, 모의실험을 수행할 때는 신뢰성 있는 난수 생성기를 사용하고, 충분한 시뮬레이션을 반복하여 적절한 결과를 얻는 것이 중요합니다.
무작위 표본 추출에 유용한 함수는 sample( ) 입니다.
sample(x, size, replace= T/F , prob= NULL)
x : 추출할 데이터 샘플
size : 추출할 표본 크기(추출횟수)
replace : TRUE 면 복원추출 , FALSE 면 비복원추출
prob : 추출확률, 기본값은 균등분포
◈ 예제 : 확률분포가 다음과 같을 때
| x | 0 | 1 | 2 |
| P(X=x) | 25 | 25 | 15 |
몬테카를로 모의 실험으로 두 개의 확률표본을 추출하는 코드는 아래와 같습니다.
x <- c(0,1,2)
probx <- c(2/5,2/5,1/5)
n <- 10
x1 <- sample(x,n,replace=T,prob=probx)
x2 <- sample(x,n,replace=T,prob=probx)
cbind(x1,x2) x1 x2
[1,] 2 2
[2,] 0 2
[3,] 1 1
[4,] 2 1
[5,] 0 0
[6,] 0 2
[7,] 0 1
[8,] 0 1
[9,] 0 0
[10,] 0 1
10개의 표본을 구해봤습니다. 매번 실행할 때마다 다른 결과가 나옵니다.
이제 횟수를 100,000번으로 해서 두 표본의 평균의 분포를 그래프로 그리면,
x <- c(0,1,2)
probx <- c(2/5,2/5,1/5)
n <- 100000
x1 <- sample(x,n,replace=T,prob=probx)
x2 <- sample(x,n,replace=T,prob=probx)
xx <- cbind(x1,x2)
xbar <- rowMeans(xx)
xbartbl <- table(xbar)/n
plot(xbartbl,type="h",xlab=expression(bar(x)),ylab=expression(f(bar(x))),col='blue')
abline(h=0)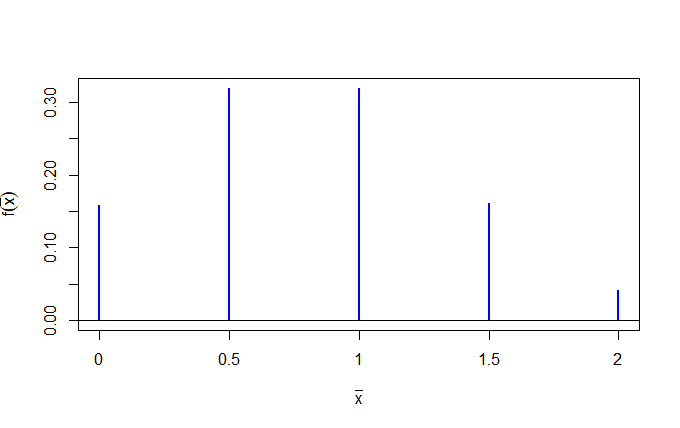
모의실험 결과
0 0.5 1 1.5 2
0.15903 0.31941 0.31978 0.16058 0.04120
이론적인 결과
0.16 0.32 0.32 0.16 0.04
모의 실험 결과가 이론적인 결과에 근접함을 볼 수 있습니다.
3. 대수의 법칙 & 중심극한정리
대수의 법칙은 동일한 확률분포에서 추출한 표본의 크기가 커질수록, 그 표본의 평균이 모평균에 가까워지는 현상을 말합니다. 즉, 표본의 크기가 커질수록 표본평균과 모평균 간의 차이가 작아진다는 것을 의미합니다.
중심극한정리는 모집단이 어떤 분포를 가지더라도, 그 분포로부터 추출된 크기가 충분히 큰 표본들의 평균이 정규분포를 따른다는 정리입니다. 이는 통계적 추정, 가설 검정, 통계적 프로세스 제어 등 다양한 통계 분야에서 중요하게 사용됩니다.
중심극한정리는 표본의 크기가 충분히 크다면, 모집단의 분포가 무엇이든 상관없이 표본평균의 분포가 정규분포에 가까워진다는 것을 의미합니다. 따라서 통계학에서는 표본의 크기를 충분히 크게 잡아줌으로써 정규분포를 가정할 수 있게 되며, 이를 기반으로 가설검정 등을 수행합니다.
대수의 법칙은 표본의 크기가 커질수록 추정치의 정확도가 중가하는 것을 나타내고, 중심극한정리는 표본의 크기가 커질수록 추정치의 분포가 정규분포에 가까워지는 것을 나타냅니다. 이러한 개념들은 통계학에서 중요한 개념이며, 실제 데이터 분석에서 표본크기를 결정하는 데에 활용됩니다.
표본추출함수
◈ 예제 : 확률분포가 다음과 같을 때
| x | 0 | 1 | 2 |
| P(X=x) | 25 | 25 | 15 |
표본을 각각 1개,10개, 50개 추출하여 100,000번 모의실험을 하면,
x <- c(0, 1, 2)
probx <- c(2/5, 2/5, 1/5)
mu <- 0.8
sigma <- sqrt(14/25)
rn <- 100000
n_vec <- c(1, 10, 50)
par(mfrow=c(1,length(n_vec))) # 그래프를 가로 방향으로 나열
for (j in 1:length(n_vec)) {
n <- n_vec[j]
xbar <- rep(NA, rn)
for (i in 1:rn) {
xbar[i] <- sum(sample(x, n, replace=T, prob=probx))
}
fx <- table(xbar) / rn
plot(fx, xlab="합", ylab="f(합)", main=paste("n=", n))
abline(h=0)
}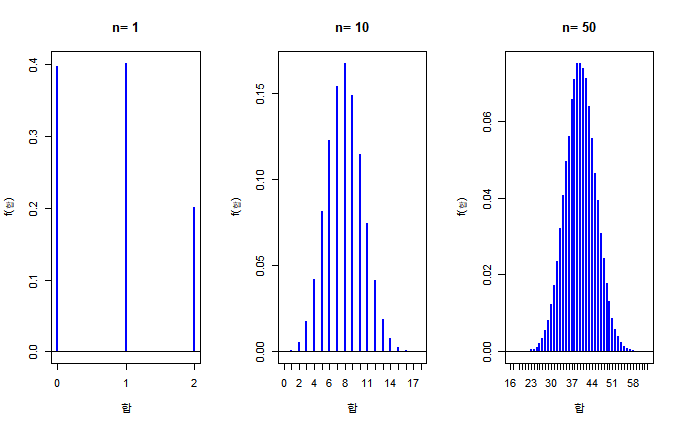
위 50개 추출한 합의 결과에 정규분포곡선과 같이 표현하면,
x <- c(0,1,2)
probx <- c(2/5,2/5,1/5)
mu <- 0.8
sigma <- sqrt(14/25)
rn <- 100000
n <- 50
xbar <- rep(NA,rn)
for (i in 1:rn)
xbar[i] <- sum(sample(x,n,replace=T,prob=probx))
fx <- table(xbar)/rn
plot(fx,xlab="합",ylab="f(합)",col='skyblue')
abline(h=0)
xx <- seq(0,n*2,by=0.01)
lines(xx,dnorm(xx,n*mu,sqrt(n)*sigma),col="red")
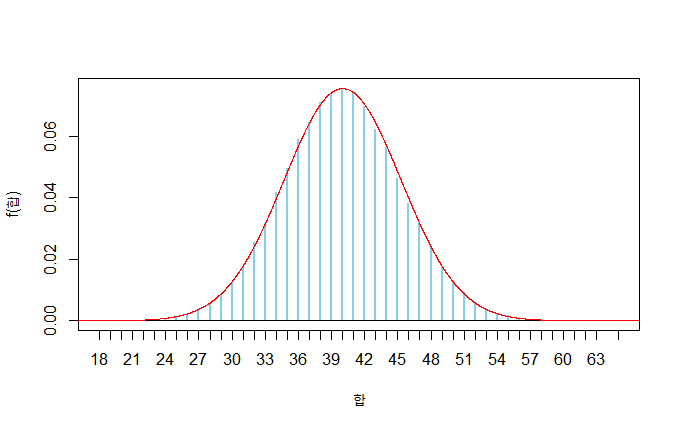
'통계학 이야기' 카테고리의 다른 글
| 57. R을 이용한 이항분포의 정규근사 (0) | 2023.12.14 |
|---|---|
| 56. 이항분포의 정규근사 (1) | 2023.12.07 |
| 54. 표집분포와 대수의 법칙 그리고 중심극한정리 (0) | 2023.11.20 |
| 53. 표집분포와 확률표본 그리고 통계량 (0) | 2023.11.16 |
| 52. R을 이용한 확률분포 - 정규분포 구하기 (0) | 2023.11.15 |




