생각 작업실 The atelier of thinking
56. 이항분포의 정규근사 본문
Chapter 56. 이항분포의 정규근사
1. 이항분포의 정규근사란?
이항분포는 대표적인 이산형 확률분포이지만, 표본크기가 충분히 크고 파라미터 값이 적당한 경우에는 정규분포로 근사할 수 있습니다. 이러한 근사를 사용하면, 이항분포를 다루기 어려운 경우에도 정규분포의 성질을 활용하여 다양한 추론을 수행할 수 있습니다.
특히, 정규분포의 선형성과 대칭성, 표준화 등의 성질을 이용하면 이항분포에 대한 확률계산이 간단하고 직관적으로 이루어집니다. 이러한 이율, 이항분포의 정규근사는 통계적 추론에서 매우 중요한 역할을 합니다.
이항분포의 정규근사는 중심극한정리를 기반으로 합니다.
2. 이항분포의 정규근사
모든 이항분포가 정규근사가 가능한 것이 아니라 조건이 어느 정도 갖추어졌을 때 정규근사를 이룰 수 있습니다.
(1) 포아송 근사
앞서 포아송분포에서 $X \sim B( n, p )$인 이항분포에서
n이 크고 p가 작은 이항분포의 경우 포아송 분포와 차이가 거의 없다는 것을 알아봤습니다.
$\lambda$ 가 5 이하이면 포아송 근사가 잘 이루어집니다.
2023.10.27 - [통계학 이야기] - 46. 포아송분포(Poisson Distribution) - 이산확률분포
46. 포아송분포(Poisson Distribution) - 이산확률분포
Chapter 45. 포아송분포(Poisson Distribution) 1. 포아송분포(Poisson Distribution)의 정의 포아송분포는 단위시간 동안 혹은 단위공간에서 어떤 사건이 발생하는 횟수를 나타내는 이산확률분포입니다. 포아
thinking-atelier.tistory.com
그러나, $p$가 0.5 에서 많이 벗어나지 않는 경우에는 포아송 근사가 잘 이루어지지 않습니다.
◈ 예제 : $ X \sim B(100,0.4)$ 인 이항분포의 기대값 $E(X) = 40$ 일 때,
$ P( X \leq 35)$ 를 구한다면?
이항분포
$$P(X \leq 35) = \sum_{x=0}^{35} \binom{100}{x} 0.4^x 0.6^{100-x} = 0.1795 $$
포아송 근사
$$ \sum_{x=0}^{35} \frac{e^{-40} 40^x}{x!} = 0.2424 $$
$p$ 가 0.5 근처라서 포아송 근사가 잘 이루어지지 않습니다.
(2) 정규근사
이항분포 $ X \sim B( n,p ) $ 에서의 기대값과 분산은 ,
$$ X = X_1+X_2+\cdots + X_n 일 때, E(X) = np , Var(X) = np(1-p) $$
입니다. 이를 표본비율로 나타낸다면, 표본비율 $ \hat{p} = \frac{X}{n} = \bar{X} $ 입니다.
따라서, 표본비율의 기대값과 분산은,
$$ E(\hat{p}) = p , Var(\hat{p}) = \frac{Var(X)}{n} = \frac{p(1-p)}{n} $$
중심극한정리에 따르면 n이 큰 경우 표본평균 값의 분포는 정규분포에 가까워 집니다.
따라서, 표본비율 $ \hat{p} $ 도 n이 꺼지면 정규분포에 근사합니다.
$$ \hat{p} \simeq N \left( p , \frac{p(1-p)}{n} \right) $$
위 식을 표준화를 하게 되면,
$$ \frac{\hat{p} - p}{\sqrt{p(1-p)/n}}\simeq N( 0, 1 ) $$
표준화된 식의 분자, 분모에 n을 곱해 정리하면,
$$ \frac{X - np}{\sqrt{np(1 - p)}} \simeq N( 0, 1 ) $$
위 식을 X로 정리하면,
$$ X \simeq N( np, np(1 - p)) $$
즉, X는 정규분포에 근사한다는 것을 보여줍니다.
▶ $X \sim B(100, 0.04)$ 와 $X \sim B(100, 0.4)$ 의 분포 비교

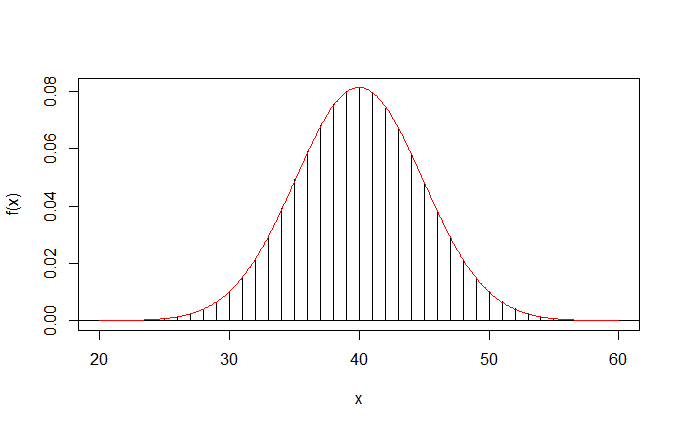
p 가 0.5에 가까울 때 정규근사가 더 잘되는 것을 보여줍니다.
3. 연속성 수정(Continuity Correction)
이항분포의 정규근사에서 연속성 수정(continuity correction)은 이항분포의 확률을 정규분포로 근사하는 경우 발생하는 근사오차를 보정하기 위한 방법입니다.
이항분포는 이산형 확률분포로 특정한 변수가 가질 수 있는 값들이 이산적이며, 반면에 정규분포는 연속형 확룰분포로 특정한 확률변수가 가질 수 있는 값들이 연속적입니다. 이러한 차이 때문에 이항분포의 확률을 정규분포로 근사화할 때, 근사 오차가 발생하게 됩니다.
이산분포인 경우 확률
$$ P( X \leq x-1 ) = P( X< x) \not= P( X \leq x ) $$
정규분포인 경우 확률
$$ P \left( Z \leq \frac{x-1-np}{\sqrt{np(1-p)}} \right) \not= P \left( Z < \frac{x-np}{\sqrt{np(1-p)}} \right) = P \left( Z \leq \frac{x-np}{\sqrt{np(1-p)}} \right) $$
$X \sim B( n, p ) $ 일 때, $ x= 0,1, ..., n$ 에 대해, $P(X>x) = P(X \ge x+1), P(X \ge x) = P(X>x-1) $이므로,

연속성 수정은 이항분포 x 값에서 1/2 만큼 더하거나 빼서 수정하게 됩니다.
$$ P( X<x ) \simeq P \left( Z < \frac{x-1/2 - np}{\sqrt{np(1-p)}} \right) \simeq P(X \leq x-1) $$
$$ P( X>x ) \simeq P \left( Z > \frac{x-1/2 - np}{\sqrt{np(1-p)}} \right) \simeq P(X \ge x+1) $$
◈ 예제 : 여론조사
전체 국민 60%가 A 정책에 대해 찬성한다고 했을 때, 150명을 무작위로 뽑아 찬성하는 사람의 비율을 알아보려고 할 때, 적극 찬성하는 사람이 78명 이하일 확률은 ?
위 문제를 식으로 표현하면, $ X \sim B(150,0.6) $ 일 때 $P(X \leq 78) $ 를 구하라는 것입니다.
이를 이항분포 가정하에서의 이항분포 확률을 구하면 0.0284 가 나옵니다.
위 식을 정규분포 근사로 푼다면, $ X \simeq N( np, np(1 - p)) $ 에 적용할 수 있습니다.
$ X \simeq N(90,36) $ 일 때,
$$ P(X \leq 78) \simeq P \left( Z \leq \frac{78-90}{6} \right) = 0.0228 $$
위 정규근사에 연속성 수정을 한다면,
$$ P(X \leq 78) \simeq P \left( Z \leq \frac{78+ 1/2 -90}{6} \right) = 0.0276 $$
연속성 수정을 했을 때 더 정확한 확률에 근접함을 알 수 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 58. T 분포(T - Distribution) - 연속확률분포 (1) | 2023.12.15 |
|---|---|
| 57. R을 이용한 이항분포의 정규근사 (0) | 2023.12.14 |
| 55. R 을 이용한 표집분포 & 몬테카를로 모의실험 (0) | 2023.11.24 |
| 54. 표집분포와 대수의 법칙 그리고 중심극한정리 (1) | 2023.11.20 |
| 53. 표집분포와 확률표본 그리고 통계량 (0) | 2023.11.16 |




