| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- JavaScript
- 산점도
- 분산분석
- 해운업
- 혼합효과모형
- 가설검정
- 글쓰기
- 인공지능
- 변량효과모형
- 회귀분석
- 정규분포
- 에세이
- 추정
- 오블완
- version 2
- 확률
- html
- 경제학
- version 1
- 고정효과모형
- r
- 반복있음
- 통계학
- 데이터 과학
- css
- 이항분포
- 변동분해
- 티스토리챌린지
- 이원배치 분산분석
- 반복없음
- Today
- Total
생각 작업실 The atelier of thinking
57. R을 이용한 이항분포의 정규근사 본문
Chapter 57. R을 이용한 이항분포의 정규근사
이항분포는 대표적인 이산형 확률분포이지만, 표본크기가 충분히 크고 파라미터 값이 적당한 경우에는 정규분포로 근사할 수 있습니다. 이러한 근사를 사용하면, 이항분포를 다루기 어려운 경우에도 정규분포의 성질을 활용하여 다양한 추론을 수행할 수 있습니다.
1. 이항분포의 확률이 0.5에 가까울 때
이항분포 $X \sim B(100, 0.4)$ 의 그래프를 그려보면, 아래와 같습니다.
n <- 100
p <- 0.4
mu <- n*p
sigma <- sqrt(n*p*(1-p))
x <- 0:n
fx <- dbinom(x,n,p)
plot(x,fx,ylab="f(x)",type="h",xlim=c(20,60))
abline(h=0)

위 이항분포 위에 정규분포 곡선을 그려보면,
x <- seq(20,60,by=0.1)
fx <- dnorm(x,mu,sigma)
lines(x,fx,col="red")
평균 40을 기준으로 좌우 대칭이 잘 되는 정규분포곡선 형태에 근사한 것을 볼 수 있습니다.
2. 이항분포의 확률이 작을 때
이항분포 $X \sim B(100, 0.04)$ 의 그래프를 그려보면, 아래와 같습니다.
n <- 100
p <- 0.04
mu <- n*p
sigma <- sqrt(n*p*(1-p))
x <- 0:n
fx <- dbinom(x,n,p)
plot(x,fx,ylab="f(x)",type="h",xlim=c(-10,50))
abline(h=0)
위 그래프에 정규분포곡선을 그려보면,
x <- seq(-10,50,by=0.1)
fx <- dnorm(x,mu,sigma)
lines(x,fx,col="red")
포아송 분포곡선을 그려보면,
lambda <- 100*0.04
x <- 0:100
pois <- dpois(x,lambda)
names(pois)<-x
barplot(pois,space=10,xlab="x",ylab="f(x)")
abline(h=0)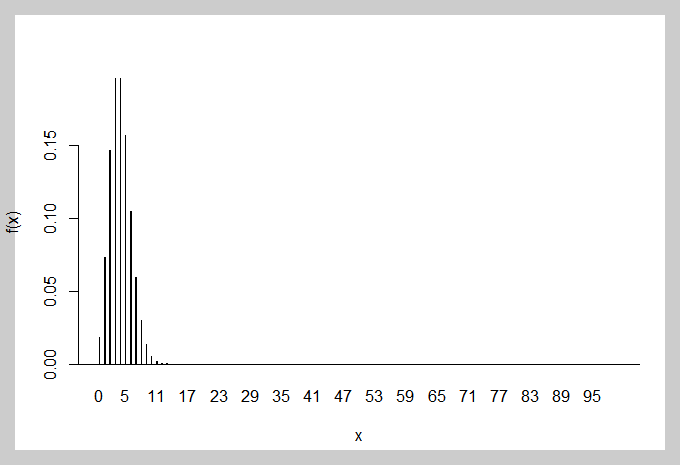
※ 확률이 0에 근접하였을 때는 포아송분포와 근사함을 알 수 있습니다.
3. 연속성 수정
◈ 예제 : 여론조사
전체 국민 60%가 A 정책에 대해 찬성한다고 했을 때, 150명을 무작위로 뽑아 찬성하는 사람의 비율을 알아보려고 할 때, 적극 찬성하는 사람이 78명 이하일 확률은 ?
위 문제를 식으로 표현하면, $ X \sim B(150,0.6) $ 일 때 $P(X \leq 78) $ 를 구하라는 것입니다.
이를 이항분포 가정하에서의 이항분포 확률을 구하면 0.0284 가 나옵니다.
R 로 계산하면,
n <- 150
p <- 0.6
pbinom(78,n,p)[1] 0.02839329
위 식을 정규분포 근사로 푼다면, $ X \simeq N( np, np(1 - p)) $ 에 적용할 수 있습니다.
$ X \simeq N(90,36) $ 일 때,
$$ P(X \leq 78) \simeq P \left( Z \leq \frac{78-90}{6} \right) = 0.0228 $$
R 로 계산하면,
mu <- n*p
sigma <- sqrt(n*p*(1-p))
pnorm(78,mu,sigma)[1] 0.02275013
위 정규근사에 연속성 수정을 한다면,
$$ P(X \leq 78) \simeq P \left( Z \leq \frac{78+ 1/2 -90}{6} \right) = 0.0276 $$
R 로 계산하면,
mu <- n*p
sigma <- sqrt(n*p*(1-p))
pnorm(78+1/2,mu,sigma)[1] 0.02764015
연속성 수정을 했을 때 더 정확한 확률에 근접함을 알 수 있습니다.
'통계학 이야기' 카테고리의 다른 글
| 59. 카이제곱분포(Chi-square Distribution) - 연속확률분포 (0) | 2023.12.20 |
|---|---|
| 58. T 분포(T - Distribution) - 연속확률분포 (0) | 2023.12.15 |
| 56. 이항분포의 정규근사 (1) | 2023.12.07 |
| 55. R 을 이용한 표집분포 & 몬테카를로 모의실험 (0) | 2023.11.24 |
| 54. 표집분포와 대수의 법칙 그리고 중심극한정리 (0) | 2023.11.20 |




