| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 변동분해
- 반복없음
- 혼합효과모형
- html
- 정규분포
- 고정효과모형
- 이원배치 분산분석
- css
- 경제학
- 산점도
- r
- 추정
- 데이터 과학
- 분산분석
- 확률
- 변량효과모형
- JavaScript
- 티스토리챌린지
- 반복있음
- 회귀분석
- 오블완
- 해운업
- 가설검정
- 인공지능
- 이항분포
- 통계학
- 글쓰기
- 에세이
- version 2
- version 1
- Today
- Total
생각 작업실 The atelier of thinking
59. 카이제곱분포(Chi-square Distribution) - 연속확률분포 본문
Chapter 59. 카이제곱분포(Chi-square Distribution) - 연속확률분포
1. 카이제곱분포란?
k개의 서로 독립적인 표준정규확률변수를 각각 제곱한 다음 합해서 얻어지는 분포입니다.
k를 자유도라고 하며 카이제곱분포의 매개변수가 됩니다. 카이제곱분포는 신뢰구간이나 가설검정에서 사용합니다.
표준정규분포를 따르는 확률변수의 제곱이 자유도가 1인 카이제곱분포를 따릅니다.
Z2∼χ21
서로 독립인 카이제곱분포의 합은 역시 카이제곱분포를 따르며 이 경우 자유도는 합치기 전 각각 확률변수의 자유도의 합과 같습니다.
2. 카이제곱분포의 확률밀도함수
카이제곱분포의 확률밀도함수는 아래와 같습니다.
f(x;k)=12k/2Γ(k/2)xk/2−1e−x/2
여기에서 Γ(k/2) 는 감마함수입니다. k는 자유도 입니다.
이 함수의 그래프는 오른쪽으로 치우친 형태를 가지며, 자유도가 커질수록 정규분포에 가까워집니다.

카이제곱 분포 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 카이제곱 분포(χ제곱分布, 영어: chi-squared distribution) 또는 χ2 분포는 k {\displaystyle k} 개의 서로 독립적인 표준정규 확률변수를 각각 제곱한 다음 합해서 얻어지
ko.wikipedia.org
3. 카이제곱분포의 특징
대칭이 될 수 없습니다. 구간 자체가 0보다 커야하기 때문입니다.
자유도에 따라 다양한 형태의 그림이 나옵니다.
자유도가 크면 클수록 옆으로 더 퍼지는 형태가 나옵니다.
4. 카이제곱분포에서의 분위수

P(χ210<2.413)=0.008,P(χ210>18.866)=0.042
P(χ210<3.247)=0.025,P(χ210>20.483)=0.025
구간 추정을 할 때 구간거리가 짧은 것(빨간선)을 선호하지만, 보다시피 계산이 무척어렵습니다.
따라서 0.025가 되는 구간(파란선)을 찾아 여기에 해당하는 임계값을 사용합니다.
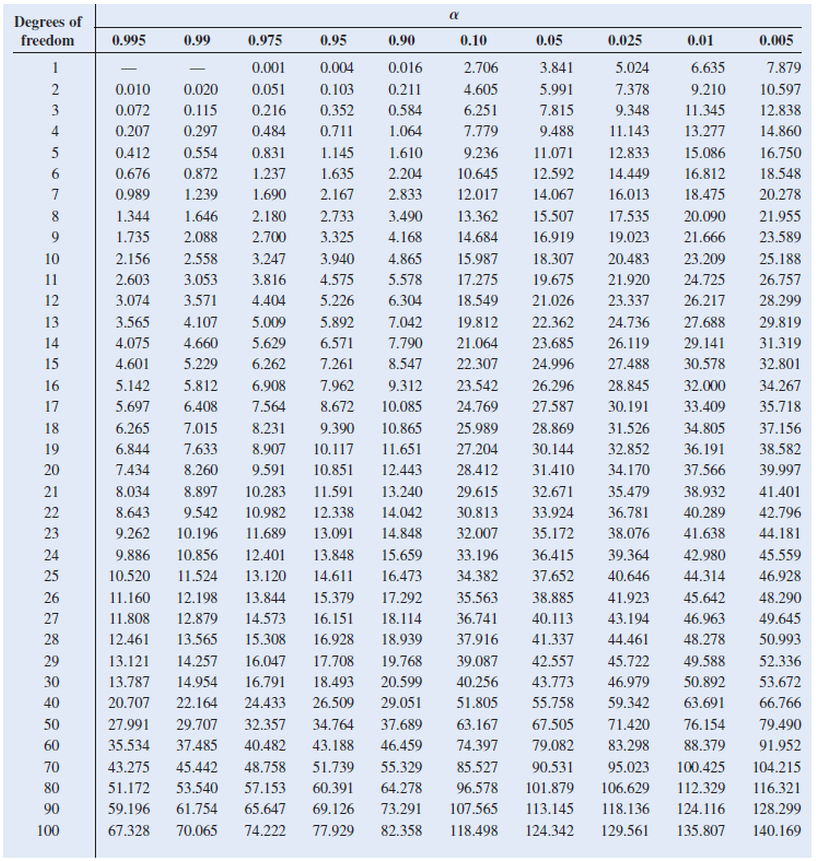
아래는 자유도에 따른 카이제곱분포표입니다.
자유도에 따른 카이제곱분포표
5. 카이제곱분포 활용
카이제곱분포는 추론통계학의 여러 분야에서 활발하게 사용됩니다. 주로 다음과 같은 분야에서 활용됩니다
(1) 가설 검정 (Hypothesis Testing)
가설 검정에서 카이제곱 분포는 주로 분할표(Contingency Table) 분석에 사용됩니다. 예를 들어, 두 범주형 변수 간의 독립성을 검정하거나 적합도 검정(Goodness of Fit Test)을 수행할 때 활용됩니다.
(2) 신뢰구간 (Confidence Intervals)
특히 분산의 신뢰구간을 추정하는 데에 사용됩니다. 분산이 정규분포를 따르지 않는 경우에도 카이제곱분포를 기반으로 한 신뢰구간을 계산할 수 있습니다.
(3) 분산 분석 (Analysis of Variance, ANOVA)
그룹 간의 평균 차이를 검정하는 ANOVA에서 오차 제곱합에 기반하여 카이제곱분포를 사용할 수 있습니다.
(4) 적합도 검정 (Goodness of Fit Tests)
표본 데이터가 어떤 이론적인 분포와 적합한지를 검정하는 데에 사용됩니다. 이는 주로 특정 분포에 대한 가정을 확인하는 데에 활용됩니다.
(5) 독립성 검정 (Test of Independence)
두 범주형 변수 간의 독립성을 확인하는 데에 사용됩니다. 이는 예를 들어 설문조사 데이터에서 변수 간의 독립성을 검정하는 데에 활용될 수 있습니다.
카이제곱분포는 주로 이러한 통계적 검정에서 오차의 분포를 모델링하는 데에 사용되며, 이러한 분석은 풍부한 통계적 정보를 제공하여 의사결정에 도움을 줍니다.
'통계학 이야기' 카테고리의 다른 글
| 61. 추정(Estimation) - 점 추정(Point Estimation) (0) | 2023.12.25 |
|---|---|
| 60. 통계적 추론(추론 통계학)의 개요 (2) | 2023.12.22 |
| 58. T 분포(T - Distribution) - 연속확률분포 (0) | 2023.12.15 |
| 57. R을 이용한 이항분포의 정규근사 (0) | 2023.12.14 |
| 56. 이항분포의 정규근사 (1) | 2023.12.07 |




