생각 작업실 The atelier of thinking
58. T 분포(T - Distribution) - 연속확률분포 본문
Chapter 58. T 분포(T-Distribution)
1. T 분포의 유래 및 원리
T-분포는 student T-분포의 줄임말로 맥주회사 기네스사에 일하던 월리엄 고셋( William Sealy Gosset )이 1908년에 제안하였는데 회사의 방침에 따라 본명을 사용할 수 없었던 고셋이 "student"라는 필명을 사용하여 제안하였습니다. 그는 작은 표본 크기에 대한 신뢰구간과 가설검정에 관한 분포를 연구하면서 T-분포를 개발했습니다.
T-분포는 정규분포와 유사하지만, 표본 크기가 작을 때 발생하는 표본평균에 대한 불확실성을 더 잘 반영합니다. 특히, T-분포는 모집단이 정규분포를 따를 때, 작은 표본에서 표본평균의 분포를 나타냅니다.
T-분포는 모집단의 표준편차를 알지 못할 때, 모집단이 정규분포를 따르는 경우에 사용합니다. 표본의 크기가 작을수록 모집단의 표준편차를 정확하게 추정하기 어렵기 때문에, 이러한 상황에서 T-분포를 사용하여 통계적 추론을 수행합니다.
T-분포는 자유도(degree of freedom)라는 개념에 기반하여 정의됩니다. 자유도는 표본의 크기에 따라 결정되며, 표본 크기가 작을수록 자유도가 작아집니다. T-분포는 표본 크기가 커질수록 표준정규분포에 수렴하게 되며, 표본 크기가 작을 때는 보다 두꺼운 꼬리(tail)를 가진 분포를 보이게 됩니다.
T-분포는 평균이 0 이고 표준편차가 1 인 표준정규분포를 따르는 확률변수를 자유도로 나눈 분포로 정의됩니다. 이러한 정의에 따라 T-분포의 확률밀도함수는 자유도에 따라 달라지며, T-분포의 특성을 나타내는 t-값을 계산하여 가설 검정 등의 통계적 추론을 수행합니다.
2. T-분포의 확률밀도함수
T-분포는 평균이 0 이고 표준편차가 1 인 표준정규분포를 따르는 확률변수를 자유도로 나눈 분포로 정의됩니다.
모집단이 평균은 $\mu$이고 분산이 $\sigma^2$인 정규분포에서 확률표본을 추출하였을 때,
$$ X_1,X_2, ... , X_n \sim iid N(\mu, \sigma^2) 이면 $$
모집단의 표준편차를 알고 있을 때 표준화를 한다면, 아래와 같습니다.
$$ Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} $$
하지만, T분포에서는 모집단의 표준편차를 모르기 때문에 대신 표본표준편차를 이용하여 표준화를 합니다.
모집단의 표준편차 대신 표본표준편차를 이용한 표준화는 아래와 같습니다. ( $\sigma$ → $S$ )
$$ T = \frac{\bar{X} - \mu}{S/\sqrt{n}} \sim t_{n-1} $$
T-분포의 확률밀도함수는 자유도에 따라 달라집니다. 따라서, T-분포의 확률밀도함수는 아래와 같습니다.
$t_{\nu}$ : 자유도가 $\nu$인 t-분포
$$ f(x) = \frac{\varGamma((\nu + 1) /2 )}{\varGamma(\nu/2)\sqrt{\nu \pi} (1+x^2/\nu)^{(\nu+1)/2} }$$
T-분포의 그래프는 아래와 같이 나타납니다.
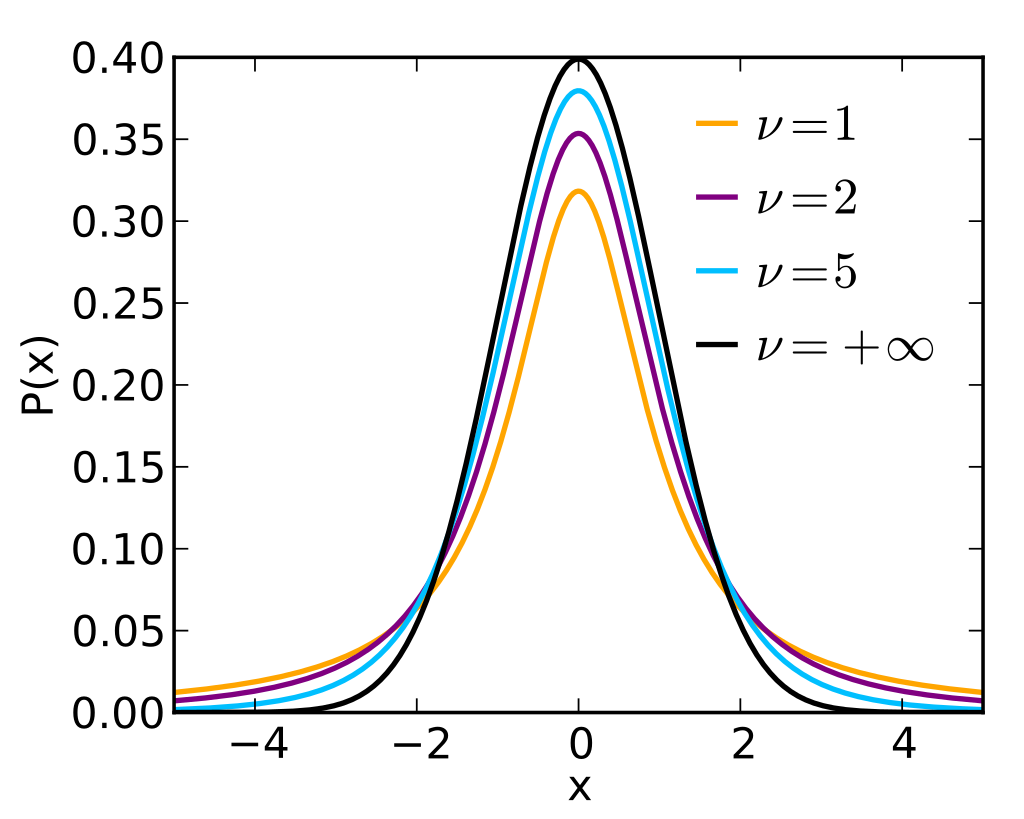
출처 : 위키백과
T-분포는 정규분포와 비슷한 모양으로 0을 중심으로 대칭이며 꼬리부분이 보다 두터운 모양을 가집니다.
전체면적이 1이 되어야 되기 때문에 가운데 부분이 낮아지면 꼬리부분이 두꺼워집니다.
T-분포의 모수는 자유도 하나이며 자유도가 커질수록 정규분포와 흡사한 모양을 가지게 됩니다.
3. T-분포 확률 및 분위수 계산

T-분포의 경우에는 자유도에 따라 다양한 확률을 가지고 있기 때문에 하나의 표로 모든 확률을 표시할 수 없습니다.위 T-분포의 확률밀도함수를 손으로 계산하는 것은 너무나 어렵습니다. 따라서 R 등 통계프로그램을 이용해 확률을 확인해 볼 수 있을 것입니다.
4. T-분포의 활용
T-분포는 모집단의 분산(혹은 표준편차)이 알려져 있지 않은 경우에 정규분포 대신 이용하는 확률분포입니다.T-분포도 표본평균, 표본분산으로 정의되는 확률분포이기 때문에 표본의 수가 많아질수록 '중심극한정리'에 의해 결국 정규분포에 수렴하게 됩니다.T-분포는 정규분포의 평균을 측정할 때 주로 사용됩니다. 즉, 모평균에 대한 통계적 추론에 T-분포를 사용합니다.
확률분포의 분류

'통계학 이야기' 카테고리의 다른 글
| 60. 통계적 추론(추론 통계학)의 개요 (2) | 2023.12.22 |
|---|---|
| 59. 카이제곱분포(Chi-square Distribution) - 연속확률분포 (0) | 2023.12.20 |
| 57. R을 이용한 이항분포의 정규근사 (0) | 2023.12.14 |
| 56. 이항분포의 정규근사 (1) | 2023.12.07 |
| 55. R 을 이용한 표집분포 & 몬테카를로 모의실험 (0) | 2023.11.24 |




